the code for the picture above has been written below, provide test cases for the code

double check if the code meets the requirements of the assignment

from __future__ import annotations

#from array_stack import ArrayStack, empty_stack, push, pop, peek, is_empty, size

from array_stack import *

import re

class PostfixFormatException(Exception):

pass

# NOTE: You'll probably need to import some things from array_stack.

def postfix_eval(input_str: str) -> float:

"""Evaluates a postfix expression"""

"""Input argument: a string containing a postfix expression where tokens are space separated. Tokens are either operators + - * / ** > or numbers

(integers or floats)

Returns the result of the expression evaluation.

Raises an PostfixFormatException if the input is not well-formed"""

stack = ArrayStack(4)

tokens = input_str.split() # isolate tokens by removing spacing

ops = "+ - * / ** >" # various operators that can be used in this function

if input_str == '': # if the input is not equal to anything raise PostfixFormatException('Insufficient operands')

raise PostfixFormatException('Insufficient operands')

for token in tokens:

if token in ops.split(" "):

try:

num2 = stack.pop() # second number is always popped before the

num1 = stack.pop()

except IndexError: # if stack has no more tokens, raise

raise PostfixFormatException('Insufficient operands')

if token == '+': # add the two nums and push it back to the stack

stack.push(num1 + num2)

elif token == '-': # subtract the two nums and push it back to the stack

stack.push(num1 - num2)

elif token == '*': # multiply the two nums and push it back to the stack

stack.push(num1 * num2)

elif token == '/': # divide the two nums and push it back to the stack

if num2 == 0:

raise ValueError('Cannot divide by 0!')

stack.push(num1 / num2)

elif token == '**': # push num1 times itself, num2 times to stack

stack.push(num1 ** num2)

elif token == '

# if num1 and num2 are floats raise bit shift exception

if type(num1) == float or type(num2) == float:

raise PostfixFormatException('Illegal bit shift operand')

# push num1 / 2**num2 or num1

stack.push(num1

elif token == '>>':

# if num1 and num2 are floats raise bit shift exception

if type(num1) == float or type(num2) == float:

raise PostfixFormatException('Illegal bit shift operand')

# push num1 * 2**num2 or num1 >> num2 to stack

stack.push(num1 >> num2)

# if the token is an operand, push it to the stack

elif token.lstrip('-').replace('.', '', 1).isdigit():

if '.' not in token:

stack.push(int(token))

else:

stack.push(float(token))

else:

raise PostfixFormatException('Invalid token')

postFix = stack.pop()

if not stack.is_empty():

raise PostfixFormatException('Too many operands')

return postFix

def infix_to_postfix(input_str: str) -> str:

"""Converts an infix expression to an equivalent postfix expression"""

"""Input argument: a string containing an infix expression where tokens are space separated. Tokens are either operators + - * / ** > or numbers

(integers or floats)

Returns a String containing a postfix expression """

stack = ArrayStack(30) # "You may assume a capacity of 30 for the Stack"

postFix = '' # initialize postFix such tokens can be added to it

tokens = input_str.split() # isolate tokens by removing spacing

priority = {'+': 0, '-': 0, '*': 1, '/': 1, '**': 2, '>': 3} # set the priorities of operators

ops = "+ - * / ** >"

if input_str == '': # if the input is not equal to anything raise PostfixFormatException('Insufficient operands')

raise PostfixFormatException('Insufficient operands')

for token in tokens:

# if token is an operand, add to RPN

if postFix == '' and token.lstrip('-').replace('.', '', 1).isdigit():

postFix += token

# if token is an operand, add to RPN

elif token.lstrip('-').replace('.', '', 1).isdigit():

postFix += ' ' + token

# if token is '(', add to stack

elif token == '(':

stack.push(token)

elif token in ops.split(" "):

if not stack.is_empty():

op2 = stack.peek()

# while the stack isn't empty, use operator priorities to formulate postfix expression

# push operators in this order: > ** * / + -

while stack.size() > 0:

op2 = stack.peek()

# if token is ')', pop operators off the stack until top of stack is '('

if op2 == '(':

break

if token == '**':

if priority[token]

postFix += ' ' + stack.pop()

else:

break

elif priority[token]

postFix += ' ' + stack.pop()

else:

break

stack.push(token)

elif token == ')':

op2 = stack.peek()

while op2 != '(':

postFix += ' ' + stack.pop()

if not stack.is_empty():

op2 = stack.peek()

stack.pop()

# When you get to the end of the infix expression, pop (and append to the RPN expression) all remaining operators

while not stack.is_empty():

postFix += ' ' + stack.pop()

return postFix # return final expression, postFix

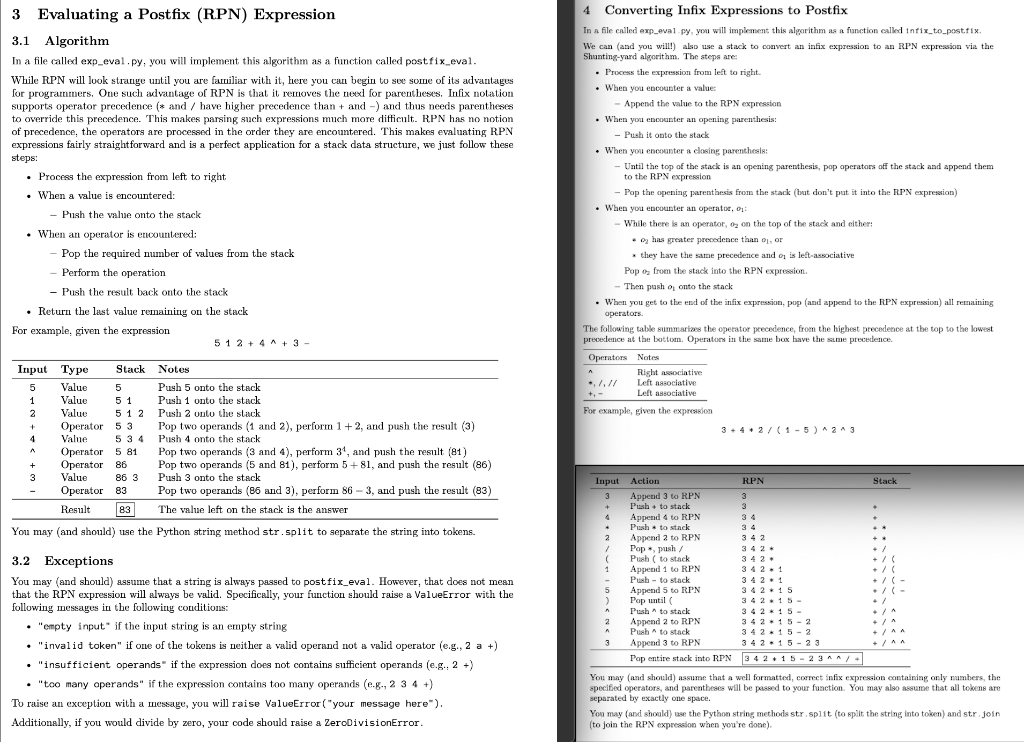
3 Evaluating a Postfix (RPN) Expression 4 Converting Infix Expressions to Postfix 3.1 Algorithm In a file called exp_eval py, you will implement this algorithm as a function calked intix_to_post.fix. In a file called exp_eval py, you will implement this algorithm as a function called postfix eeval. We can (and youl will) also use a stack to convert an infix expression to an RPN expression via the Shunting-yard algorithm. The steps are: While RPN will look strange until you are familiar with it, here you can begin to see some of its advantages - Process the expression from leet to right. for programmers. One such advantage of RPN is that it removes the neox for parentheses. Infix notation - When you encounter a value: supports operator precedence (* and / have higher precedence than + and ) and thus needs parentheses - Append the value to the RPN expression to override this precedence. This makes parsing such expressions much more difficult. R.PN has no notion - When you encounter an opening parenthesis: of precedence, the operators are processed in the order they are encountered. This makes evaluating RPN - Push it onto the stack expressions fairly straightforward and is a perfect application for a stack data structure, we just follow these steps: - When you encounter a clasing parenthesls: - Process the expression from left to right - Until the top of the stack is an opening parenthesis, pop opernators off the stack and append them - When a value is encountered: - Pop the opening parenthesis from the stark (bat don't put it into the R.PN expression) - Push the value onto the stack - When you eacouster an operator, 1: - When an operator is encountered; - While there is an operator, o2 on the top of the stack and either: - Pop the required number of values from the stack - o2 has greater precodence than o1, or - Perform the operation * they have the same precedence and q1 is leet-associative - Push the result back onto the stack Pop on from the stack into the RPN expresion. - Tben push o1 onto the stack - Return the last value remaining on the stack - When you get to the end of the infix expressian, pop (and append to the RPN expression) all remaining operators. For example, given the expression 512+4+3 The following table summarises the operator precedence, from the highest precedence at the top to the lawert precedence at the botiom. Operators in the same box have the same precedence. For example, given the expreasion 3+4+2/(15)23 You may (and should) wse the Python string method str.split to separate the string into tokens. 3.2 Exceptions You may (and should) assume that a string is always passed to postfin_eval. However, that does not mean that the RPN expression will always be valid. Specifically, your function should raise a ValueError with the following messages in the following conditions: - "empty input" if the input string is an empty string - "inval id token" if one of the tokens is neither a valid operand not a valid operator (e.g., 2 a +) - "insufficient operands" if the expression does not contains sufficient operands (e.g., 2 +) - "too many operands" if the expression contains too many operands (e.g., 234 +) To raise an exception with a message, you will raise ValueError ("your message here"). You may (and should) assume that a well formatted, correct infix cxpreseion containiag only numbers, the specifed operaters, and parentbeses will be passed to your function. You may also assume that all tobens are separated by exactly one space. Additionally, if you would divide by zero, your code should raise a ZerodivisionError. You may (and shoald) use the Python string methods str. split (to split the string into token) and ster. join (to join the RPN expreselon when you're done)