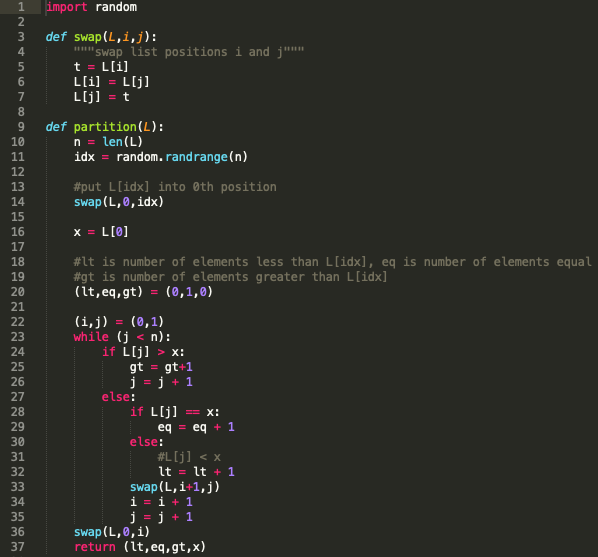
The code for the selection algorithm is written in python. As pointed out the code is incorrect because there may be multiple elements equal to the one we are partitioning around (x) and while the counts lt, eq, gt are computed correctly, the x may not necessarily occur where they should. Give an example where this incorrect code may lead to incorrect result. Also, change the code (dont change the function names etc.) to fix this. Your modified code should also run the partitioning in linear time.

import random

def swap(L,i,j):

"""swap list positions i and j"""

t = L[i]

L[i] = L[j]

L[j] = t

def partition(L):

n = len(L)

idx = random.randrange(n)

#put L[idx] into 0th position

swap(L,0,idx)

x = L[0]

#lt is number of elements less than L[idx], eq is number of elements equal

#gt is number of elements greater than L[idx]

(lt,eq,gt) = (0,1,0)

(i,j) = (0,1)

while (j

if L[j] > x:

gt = gt+1

j = j + 1

else:

if L[j] == x:

eq = eq + 1

else:

#L[j]

lt = lt + 1

swap(L,i+1,j)

i = i + 1

j = j + 1

swap(L,0,i)

return (lt,eq,gt,x)

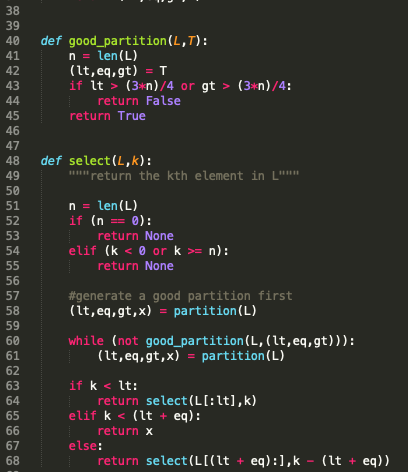
def good_partition(L,T):

n = len(L)

(lt, eq, gt) = T

if lt > (3*n)/4 or gt > (3*n)/4:

return False

return True

def select(L,k):

"""return the kth element in L"""

n = len(L)

if (n == 0):

return None

elif (k = n):

return None

#generate a good partition first

(lt,eq,gt,x) = partition(L)

while (not good_partition(L,(lt,eq,gt))):

(lt,eq,gt,x) = partition(L)

if k

return select(L[:lt],k)

elif k

return x

else:

return select(L[(lt + eq):],k - (lt + eq))

import random def swap(L,i,j): swap list positions i and jo t = L[i] L[i] = L[j] L[j] = t def partition(L): n = len(L) idx = random. randrange(n) #put L[idx] into @th position swap(L, 0, idx) x = L[0] #It is number of elements less than L[idx), eq is number of elements equal #gt is number of elements greater than L[idx] (lt, eq,gt) = (0,1,0) (i,j) = (0,1) while (j X: gt = gt+1 j = i + 1 else: if L[j] == x: eq = eq + 1 else: #L[j] (3*n)/4 or gt> (3*n)/4: return false return True def select(1,k): return the kth element in L n = len(L) if (n == 0): return None elif (k = n): return None #generate a good partition first (lt,eq,gt,x) = partition(L) while (not good_partition(L,(lt,eq,gt))): (lt,eq,gt,x) = partition (L) if k X: gt = gt+1 j = i + 1 else: if L[j] == x: eq = eq + 1 else: #L[j] (3*n)/4 or gt> (3*n)/4: return false return True def select(1,k): return the kth element in L n = len(L) if (n == 0): return None elif (k = n): return None #generate a good partition first (lt,eq,gt,x) = partition(L) while (not good_partition(L,(lt,eq,gt))): (lt,eq,gt,x) = partition (L) if k <>