The energy levels of a particle in a 3D box (where the potential is infinite outside the box), with equal sides in each dimension, x = y = z = , can be expressed as a function of the energy levels for each dimension:

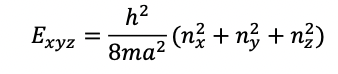
(a) Determine the states that have energy E

(b) We prepare a particle system in the 3D box with an initial state . A single measurement is made and the energy is found to be Exyz =  (17).

What is the state xyz of the system after the measurement? ()represent the quantum numbers in each dimension) What can we say about the state of the system before making the measurement?

(c) Let us set up the particle system in the 3D box with the same initial state  and measure the energy. This is done in a large number of repetitions and it is found that 75% of the measurements result with energy Exyz =  (17) and 25% of measurements result with energy Exyz =  (12). 

What is the initial state  expressed in terms of the final states !&'? How does the concept of normalization apply when writing this expression for ?

This exercise is all about Particle in a 3D Box and Quantum Measurements

Exyz = h2 (n + n} + nz) + 82 h2 8ma2 nd