The focus of the paper is on the question of whether there

is a Bayesian incentive-compatible mechanism that implements the alternative b

whenever it is efficient; that is, whenever ?1 + ?2 ? 1. This is a natural notion of

efficiency because the sum of utilities from the compromise b is ?1 + ?2, whereas

alternatives a and c each yield a utility sum of 1. To induce agents to correctly reveal

their types the mechanism designer can choose the probabilities of the individuals'

favorites, a and c, judiciously. These probabilities can be used as an instrument for

providing incentives because they are welfare neutral: Both alternatives yield exactly

the same amount of welfare.

Brgers and Postl (2009) note that their framework is equivalent to a public goods

model similar to the one we considered in Section 3.3. One can think of the "com-

promise" as a public good for which both agents have to give up probability of their

preferred alternative. The cost function is one-to-one: For each unit of the public good

(i.e., probability of the compromise) produced some agent has to give up one unit of

money (i.e., probability of their preferred alternative). An important difference with

the public goods models that we considered in Section 3.3 is that agents are liquidity

constrained: Probabilities have to be between zero and one, and therefore agents can-

not give up more than some upper bound of probability of their preferred alternative.

Using arguments similar to our arguments in Section 3.3, Brgers and Postl (2009)

show that no Bayesian incentive-compatible mechanism implements the first best?

that is, choice of the compromise with probability 1 if and only if ?1 + ?2 ? 1. The

problem of finding a second best mechanism is complicated by the fact that agents

face liquidity constraints. Therefore, to determine the second best, one cannot use the

approach that was explained in Section 3.3. Brgers and Postl (2009) have analytical

results only for small parameterized classes of direct mechanisms. They complement

these results with a numerical investigation of second best mechanisms.

The compromise problem described here is a sandbox model for the more gen-

eral model of determining an optimal voting scheme when there are three or more

alternatives?that is, the Bayesian equivalent of the problem that Gibbard and Sat-

terthwaite studied. The difficulties that we found analyzing the much simpler model

indicate that the more general problem is analytically hard and that it might benefit

from numerical investigation.

(a) Give a direct proof that efficient decision rules are cyclically monotone. (Don't

take the detour of first appealing to the fact that efficient decision rules are part of

ex post incentive-compatible mechanisms and then applying Rochet's theorem.

This would make this problem pointless.)

(b) Suppose every agent i's preferences were given by ui(a, ?i) - ?i(ti), where ?i :

R ? R is strictly increasing. Let efficient allocation rules be defined as in Defi-

nition 7.3. Can you find a modification of the payments in VCG mechanisms that

makes efficient decision rules dominant strategy incentive-compatible?

(c) Consider the problem of allocating a single indivisible good to one of two agents.

Use the setup of Section 4.2. Is there a budget-balanced dominant strategy mech-

anism that allocates the good to the agent with the higher value? Note that we

don't require the mechanism to be individually rational.

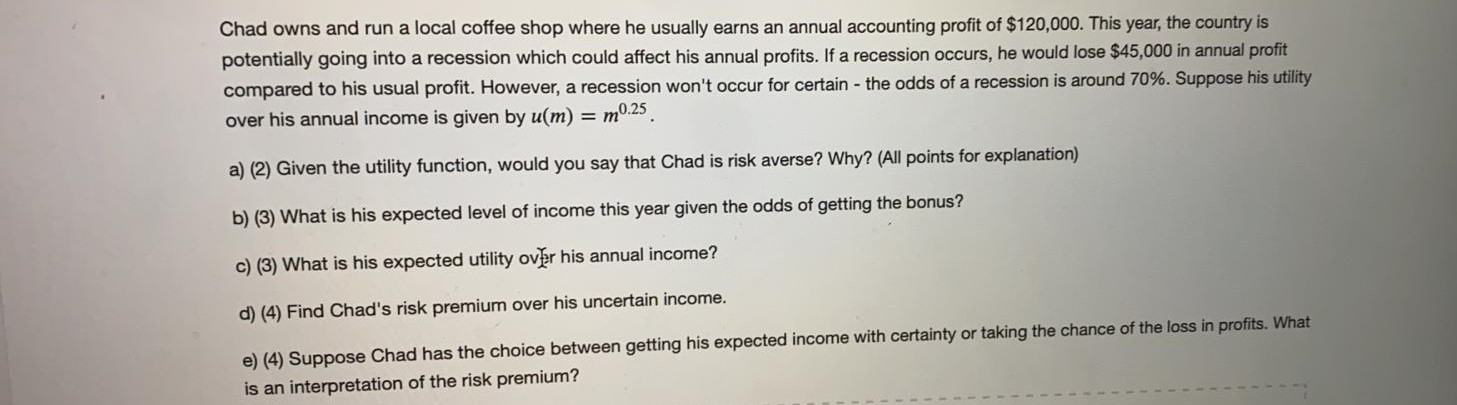
Chad owns and run a local coffee shop where he usually earns an annual accounting profit of $120,000. This year, the country is potentially going into a recession which could affect his annual profits. If a recession occurs, he would lose $45,000 in annual profit compared to his usual profit. However, a recession won't occur for certain the odds of a recession is around 70%. Suppose his utility over his annual income is given by u(m) = m0.25 a) (2) Given the utility function, would you say that Chad is risk averse? Why? (All points for explanation) b) (3) What is his expected level of income this year given the odds of getting the bonus? c) (3) What is his expected utility over his annual income? d) (4) Find Chad's risk premium over his uncertain income. e) (4) Suppose Chad has the choice between getting his expected income with certainty or taking the chance of the loss in profits. What is an interpretation of the risk premium?