Question
The following estimated regression equation was developed for a model involving two independent variables. hat(y)=40.7+8.63x_(1)+2.71x_(2) After x_(2) was dropped from the model, the least
The following estimated regression equation was developed for a model involving two independent variables.\
hat(y)=40.7+8.63x_(1)+2.71x_(2)\ After
x_(2)was dropped from the model, the least squares method was used to obtain an estimated regression equation involving only
x_(1)\ as an independent variable.\
hat(y)=42.0+9.01x_(1)\ a. Give an interpretation of the coefficient of
x_(1)in both models.\ In the two independent variable case, the coefficient
x_(1)represents the expected change in\ corresponding to a\ one unit increase in\ when\ is held constant.\ In the single independent variable case, the coefficient
x_(1)represents the expected change in\ corresponding to\ a one unit increase in\ b. Could multicollinearity explain why the coefficient of
x_(1)differs in the two models? If so, how? Assume that
x_(1)and
x_(2)are correlated.\
\\\\sqrt(-s) 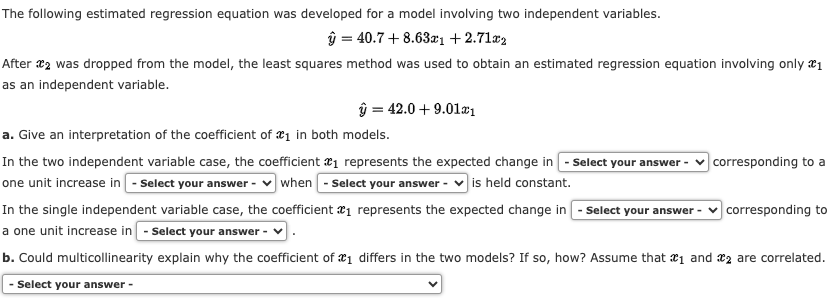
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


