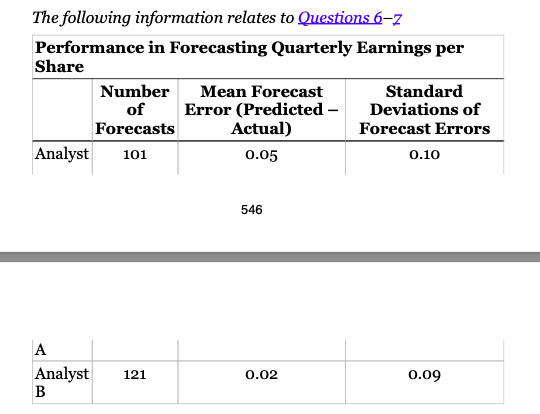


The following information relates to Questions 6-2 Performance in Forecasting Quarterly Earnings per Share Number Mean Forecast Standard of Error (Predicted - Deviations of Forecasts Actual) Forecast Errors Analyst 101 0.05 0.10 546 A Analyst B 121 0.02 0.09 6. Investment analysts often use earnings per share (EPS) forecasts. One test of forecasting quality is the zero-mean test, which states that optimal forecasts should have a mean forecasting error of o. (Forecasting error = Predicted value of variable - Actual value of variable.) You have collected data (shown in the table above) for two analysts who cover two different industries: Analyst A covers the telecom industry; Analyst B covers automotive parts and suppliers. A. With u as the population mean forecasting error, formulate null and alternative hypotheses for a zero-mean test of forecasting quality. B. For Analyst A, using both a t-test and a z-test, determine whether to reject the null at the 0.05 and 0.01 levels of significance. C. For Analyst B, using both a t-test and a z-test, determine whether to reject the null at the 0.05 and 0.01 levels of significance. 7. Reviewing the EPS forecasting performance data for Analysts A and B, you want to investigate whether the larger average forecast errors of Analyst A are due to chance or to a higher underlying mean value for Analyst A. Assume that the forecast errors of both analysts are normally distributed and that the samples are independent. A. Formulate null and alternative hypotheses consistent with determining whether the population mean value of Analyst A's forecast errors (uz) are larger than Analyst B's (uz). B. Identify the test statistic for conducting a test of the null hypothesis formulated in Part A. C. Identify the rejection point or points for the hypothesis tested 547 in Part A, at the 0.05 level of significance. D. Determine whether or not to reject the null hypothesis at the 0.05 level of significance. The following information relates to Questions 6-2 Performance in Forecasting Quarterly Earnings per Share Number Mean Forecast Standard of Error (Predicted - Deviations of Forecasts Actual) Forecast Errors Analyst 101 0.05 0.10 546 A Analyst B 121 0.02 0.09 6. Investment analysts often use earnings per share (EPS) forecasts. One test of forecasting quality is the zero-mean test, which states that optimal forecasts should have a mean forecasting error of o. (Forecasting error = Predicted value of variable - Actual value of variable.) You have collected data (shown in the table above) for two analysts who cover two different industries: Analyst A covers the telecom industry; Analyst B covers automotive parts and suppliers. A. With u as the population mean forecasting error, formulate null and alternative hypotheses for a zero-mean test of forecasting quality. B. For Analyst A, using both a t-test and a z-test, determine whether to reject the null at the 0.05 and 0.01 levels of significance. C. For Analyst B, using both a t-test and a z-test, determine whether to reject the null at the 0.05 and 0.01 levels of significance. 7. Reviewing the EPS forecasting performance data for Analysts A and B, you want to investigate whether the larger average forecast errors of Analyst A are due to chance or to a higher underlying mean value for Analyst A. Assume that the forecast errors of both analysts are normally distributed and that the samples are independent. A. Formulate null and alternative hypotheses consistent with determining whether the population mean value of Analyst A's forecast errors (uz) are larger than Analyst B's (uz). B. Identify the test statistic for conducting a test of the null hypothesis formulated in Part A. C. Identify the rejection point or points for the hypothesis tested 547 in Part A, at the 0.05 level of significance. D. Determine whether or not to reject the null hypothesis at the 0.05 level of significance









