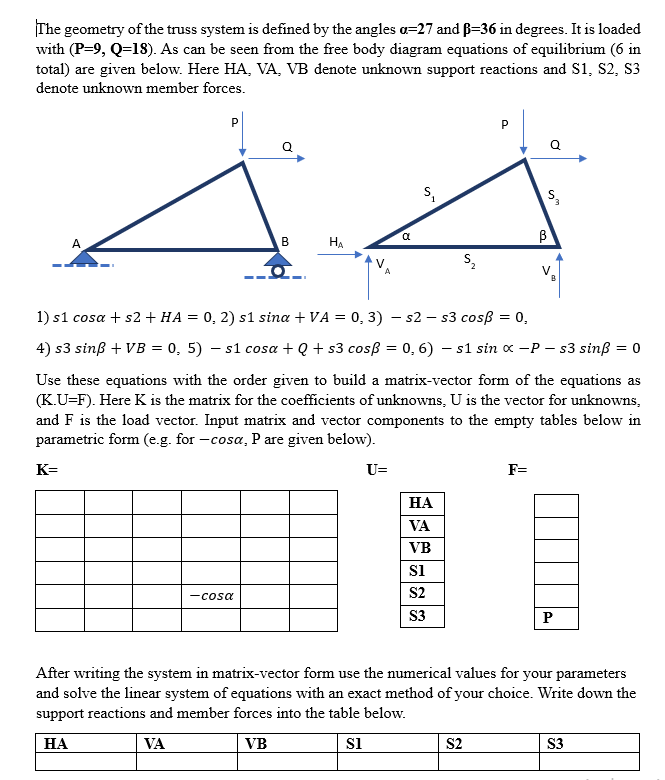The geometry of the truss system is defined by the angles =27 and =36 in degrees. It is loaded with (P=9,Q=18). As can be seen from the free body diagram equations of equilibrium ( 6 in total) are given below. Here HA, VA, VB denote unknown support reactions and S1,S2,S3 denote unknown member forces. 1) s1cos+s2+HA=0,2)s1sin+VA=0,3)s2s3cos=0, 4) s3sin+VB=0,5)s1cos+Q+s3cos=0,6)s1sinPs3sin=0 Use these equations with the order given to build a matrix-vector form of the equations as (K.U=F). Here K is the matrix for the coefficients of unknowns, U is the vector for unknowns, and F is the load vector. Input matrix and vector components to the empty tables below in parametric form (e.g. for cos,P are given below). K= U=HAVAVBS1S2S3 F= \begin{tabular}{|l|} \hline \\ \hline \\ \hline \\ \hline \\ \hline P \\ \hline \end{tabular} After writing the system in matrix-vector form use the numerical values for your parameters and solve the linear system of equations with an exact method of your choice. Write down the support reactions and member forces into the table below. The geometry of the truss system is defined by the angles =27 and =36 in degrees. It is loaded with (P=9,Q=18). As can be seen from the free body diagram equations of equilibrium ( 6 in total) are given below. Here HA, VA, VB denote unknown support reactions and S1,S2,S3 denote unknown member forces. 1) s1cos+s2+HA=0,2)s1sin+VA=0,3)s2s3cos=0, 4) s3sin+VB=0,5)s1cos+Q+s3cos=0,6)s1sinPs3sin=0 Use these equations with the order given to build a matrix-vector form of the equations as (K.U=F). Here K is the matrix for the coefficients of unknowns, U is the vector for unknowns, and F is the load vector. Input matrix and vector components to the empty tables below in parametric form (e.g. for cos,P are given below). K= U=HAVAVBS1S2S3 F= \begin{tabular}{|l|} \hline \\ \hline \\ \hline \\ \hline \\ \hline P \\ \hline \end{tabular} After writing the system in matrix-vector form use the numerical values for your parameters and solve the linear system of equations with an exact method of your choice. Write down the support reactions and member forces into the table below