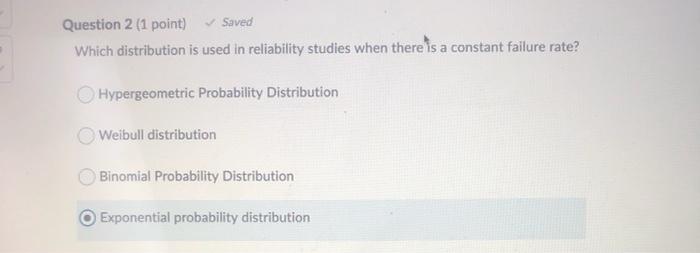
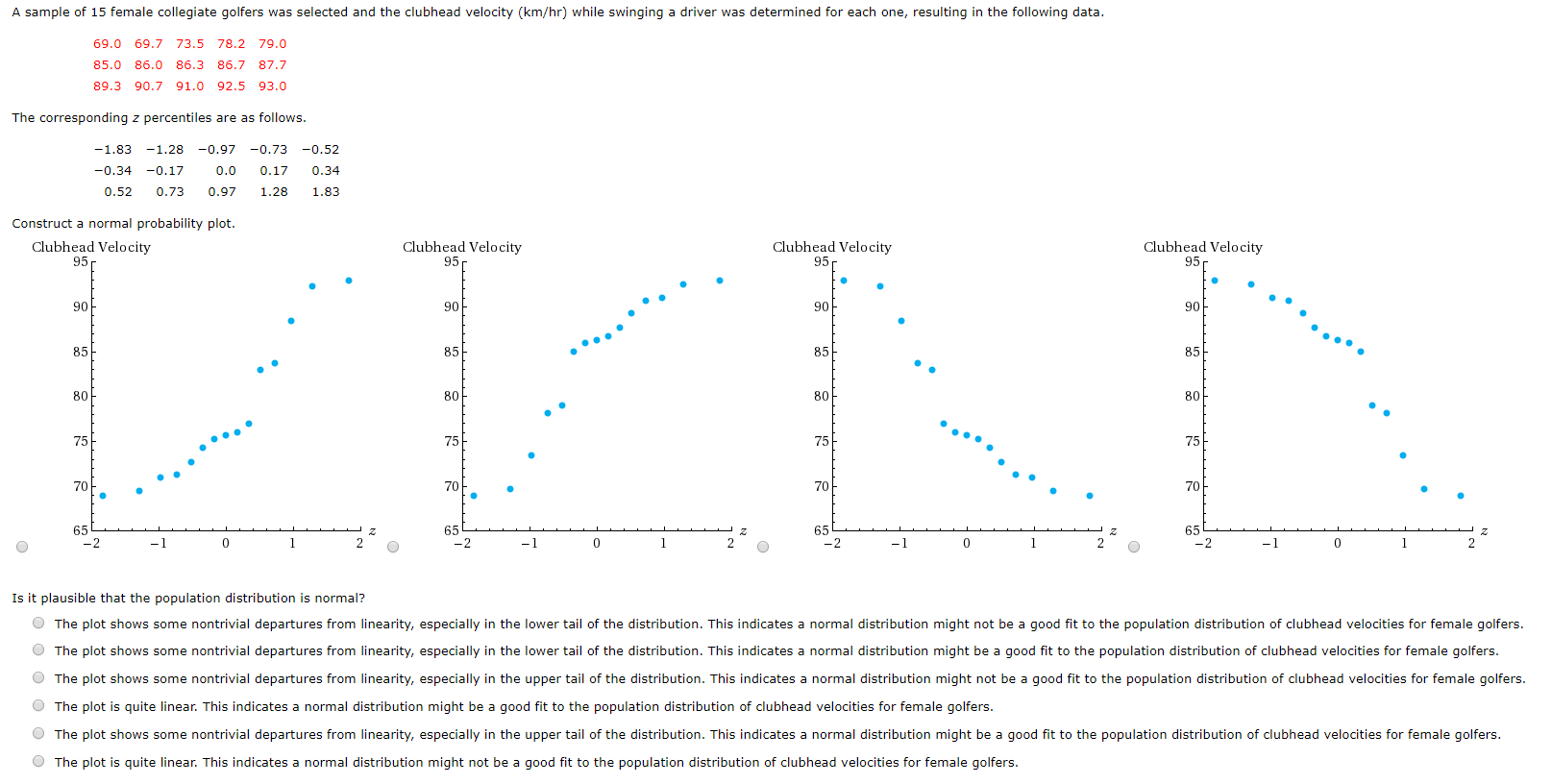
Question
The grouping of particles in a suspension is 50 for each mL. A 5 mL volume of the suspension is removed. a. What is the
The grouping of particles in a suspension is 50 for each mL. A 5 mL volume of the
suspension is removed.
a. What is the likelihood that the quantity of particles removed will be among 235 and
265?
b. What is the likelihood that the normal number of particles per mL in the pull out example
is somewhere in the range of 48 and 52?
c. In the event that a 10 mL test is removed, what is the likelihood that the normal number per mL
of particles in the removed example is somewhere in the range of 48 and 52?
d. How huge an example should be removed with the goal that the normal number of particles per mL in
the example is somewhere in the range of 48 and 52 with likelihood 95%?
In an arbitrary example of 100 batteries created by a specific technique, the normal
lifetime was 150 hours and the standard deviation was 25 hours.
(I) Find a 95% certainty span for the mean lifetime of batteries created by this
model.
(ii) Find a 99% certainty span for the mean lifetime of batteries created by this
model.
(iii) A designer asserts that the mean lifetime is somewhere in the range of 147 and 153 hours. With what
level of certainty can this assertion is made?
(iv) Approximately the number of batteries should be inspected with the goal that a 95% certainty
stretch will indicate the intend to inside 2 hours?
(v) Approximately the number of batteries should be examined so a 99% certainty
stretch will determine the intend to inside 2 hours
A Company scientist has been given the assignment of gathering data pretty much all representatives
inside the organization to more readily comprehend the adequacy of their advanced education pathway
program offered to all representatives. The likelihood that a worker has been at the organization
at least five years is 0.74, the likelihood that a representative has a Master's level certificate or
higher is 0.34, and the likelihood that an arbitrarily chosen worker has been at the organization
at least five years and has a Master's certificate is 0.12.
F. Of the individuals who have a graduate degree 35.29% have been at the organization at least 5 years
while those with lower degrees 93.94 % have been at the organization at least 5 years. Make a likelihood tree portraying the present circumstance.
Thank you kindly for responding to me. Would you be able to kindly answer the (iv) and (v) sub parts.
In an irregular example of 100 batteries delivered by a specific strategy, the normal
lifetime was 150 hours and the standard deviation was 25 hours.
(I) Find a 95% certainty span for the mean lifetime of batteries created by this
model.
(ii) Find a 99% certainty span for the mean lifetime of batteries created by this
model.
i21i
(iii) An architect guarantees that the mean lifetime is somewhere in the range of 147 and 153 hours. With what
level of certainty can this assertion is made?
(iv) Approximately the number of batteries should be tested with the goal that a 95% certainty
span will determine the intend to inside 2 hours?
(v) Approximately the number of batteries should be tested with the goal that a 99% certainty
span will determine the intend to inside 2 hours?


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


