The Monte Carlo simulation procedure is a very powerful tool which financial engineers use to price options, especially complex ones for which no closed form solutions exist. In order to value European options with this methodology, we use the following equation to simulate the terminal distribution of the price or the level of the underlying source of risk on the option's maturity date:

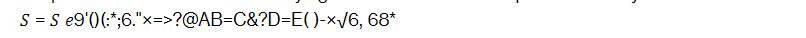
where S₀ is the spot price or the level of the underlying source of risk., T is the option's time to maturity expressed in years, r is the continuously-compounded risk-free rate, q is underlying source of risk's continuously compounded income or dividend yield, σ is the implicit volatility at which the option is trading, and NORMSINV(RAND()) is the combination of MS Excel functions which produces random draws from the standardized normal distribution.

A) Using the above equation, produce a sample consisting of 10,000 random draws to simulate the terminal distribution of a stock's price one year out. The stock is trading for $95, its continuous dividend yield is equal to 1% per year, and at-the-money options on the stock trade at an implicit volatility of 45%. The continuously compounded risk-free interest rate is equal to .5% per annum. Do not report these random draws in your paper, but report the histogram showing the stock's simulated terminal price distribution.

B) Estimate the price of a one-year European at-the-money put option on this stock using the stock's i) first 1,000, ii) first 2,000, iii) first 5,000, and iv) all 10,000 simulated terminal prices produced in A). For each option price estimate, report the estimate's standard deviation, standard error, 95% confidence lower bound, 95% confidence upper bound, and its pricing error relative to the BSM model. The standard error of the option's price estimate is equal to the standard deviation of its discounted expected terminal payoff divided by the square root of the sample size upon which the option price estimate is based. The 95% confidence interval for the true option price lies between

 ±1.96 ×  S.D.   / √numdraws where numdraws represents the sample size. Present your results in a neat table.

Transcribed Image Text:

S = S e9'0) (*;6."x=>?@AB=C&?D=E()-*√6, 68* S = S e9'0) (*;6."x=>?@AB=C&?D=E()-*√6, 68*

Answer rating: 100% (QA)

A To generate a sample of 10000 random draws for the terminal distribution of the s... View the full answer