Question
The preferences of two consumers are represented by the utility functions: The consumers, face the standard budget constraint . For each one of the utility
The preferences of two consumers are represented by the utility functions:
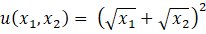
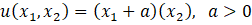
The consumers, face the standard budget constraint 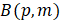 .
.
For each one of the utility functions above, derive the followings:
1) Confirm that preferences represented in by the utility function satisfy monotonicity and convexity: Derive the MRS and confirm that it is negative (monotonicity) and its absolute value is decreasing down the curve as 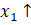 and
and 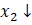 (convexity).
(convexity).
2) Derive the demand Functions. Will the solution for the consumers problem be always interior?
3) Derive the Indirect Utility Function and use Roys identity to confirm you got it right.
4) Derive the compensated demand functions, and confirm that is homogenous of degree zero in  .
.
5) Derive the expenditure functions, and confirm that it is homogenous of degree one in 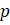 .
.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


