The price f(t,x) of a European derivative at time t when the underlying stock price is x satisfies the Black-Scholes Partial Differential Equation given by

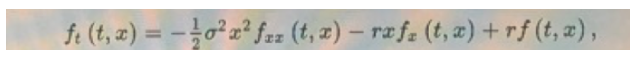
Where is stock volatility and r is the risk-free rate. This equation relates the derivative price to derivative Greeks. A stocks price is $60 and volatility is 60% per annum. The risk-free rate is 4% per annum continuously compounded. A derivative on the stock has delta of 0.8, gamma (sensitivity of delta to stock price) of 0.08, and theta (sensitivity of option price to time passage) of -8. What is the price of the derivative?

fe (t, x) = - 02.? faz (t, x) rafe (t, x) + rf (t, x)