The question is stated above. Supporting information is given below

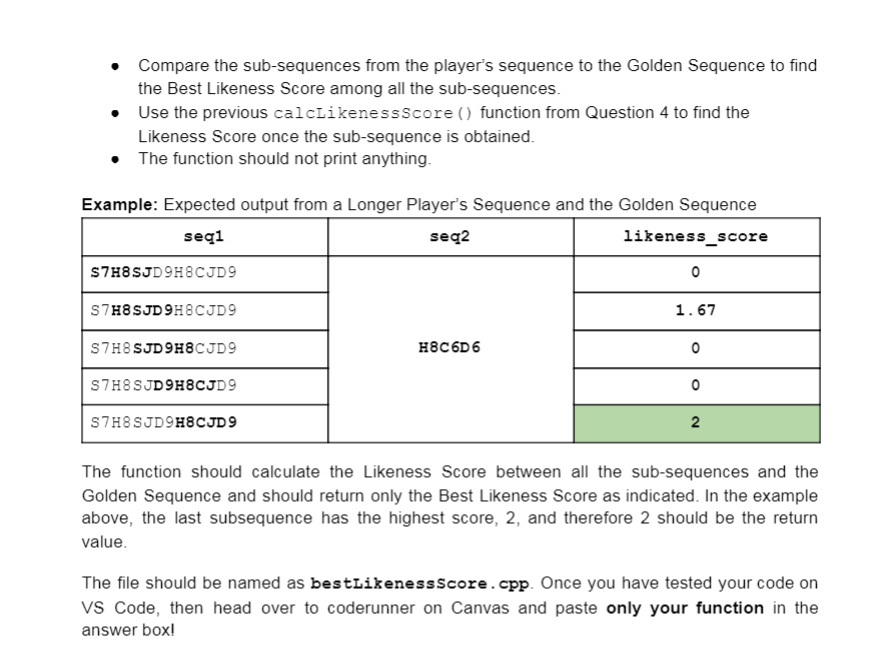
Question 5: bestLikenessScore () (8 points) Write a function called bestLikenessscore () that is going to find the best Likeness Score between all the subsequences of a sequence (whose length is greater than or equal to the Golden Sequence) and the Golden Sequence. This function finds the maximum possible score a player could have. Function Specifications: Name: bestLikenessscore () Parameters (Please Follow the same Order): o seqi (string) - The Player's Sequence (length greater than or equal to Golden Sequence) o gold_seg (string) - The Golden Sequence Return Value: Best Likeness Score - best_likeness_score (double) Length of seqi should be greater than or equal to gold_seg for the function to calculate the Best Likeness Score. If not, return -1. Compare the sub-sequences from the player's sequence to the Golden Sequence to find the Best Likeness Score among all the sub-sequences. Use the previous calcLikenessscore () function from Question 4 to find the Likeness Score once the sub-sequence is obtained. The function should not print anything. Example: Expected output from a Longer Player's Sequence and the Golden Sequence segi seg2 likeness_score S7H8SJD 9HXCJD9 0 S7H8SJD 9H8CJD9 1.67 S7H8SJD 9H8CJD9 H8C6D6 0 S7H8SJD 9H8CJD9 0 S7H8SJD 9H8CJD9 2. 2 The function should calculate the Likeness Score between all the sub-sequences and the Golden Sequence and should return only the Best Likeness Score as indicated. In the example above, the last subsequence has the highest score, 2, and therefore 2 should be the return value. The file should be named as bestLikenessScore.cpp. Once you have tested your code on VS Code, then head over to coderunner on Canvas and paste only your function in the answer box! DECK OF CARDS The standard 52-card deck of French-suited playing cards is the most common pack of playing cards used today. A standard 52-card pack comprises 13 ranks in each of the four French suits: Clubs (6), Diamonds (), Hearts () and Spades (), with reversible (double-headed) court cards (face cards). Each suit includes an Ace, a King, Queen and Jack, each depicted alongside a symbol of its suit; and numerals or pip cards from the Deuce (Two) to the Ten, with each card depicting that many symbols (pips) of its suit. Example set of 52 playing cards; 13 of each suit: clubs, diamonds, hearts, and spades 2 3 4 5 6 7 8 9 10 Jack Queen King Ace Clubs : Diamonds . . Hearts E Spades Ref: Standard 52-Card Deck SEQUENCE OF CARDS John, Mike and Suzy head to the Carnival at Zootopia. They come across a stall named "Can You Pick 'em Right?!. The stall owner Mr X greets them and invites them to play his game and tells them that the winner will get a coupon worth $50 to spend in the Carnival. The three friends get excited and decide to play the game. Mr X starts to explain the game to the participants. The ultimate aim of the game is for the players to create a sequence by picking a set of cards which is similar to the sequence picked by the host, i.e., Mr X. He says that every player is free to choose up to a maximum of 10 cards to form their sequence. A sequence is formed by the cards picked by the players. The players select a subsequence of cards from their hand to compare against the golden sequence. The players cannot rearrange the cards, but can select a continuous subset that is the same length as the golden sequence. The game is played with multiple decks of cards. We know that in a deck of cards there are four suits: Spades (S), Hearts (H), Diamonds (D) and Clubs (C). And there are 13 ranks in each suit: Ace, 2-10, Jack, Queen and King. For the purpose of creating the sequence Ace is treated as the character A, Ten as T, Jack as J, Queen as Q and King as K. Formation of Sequences: First, the card's suit is taken and the letter representing that suit is added to the sequence. Next, the card's rank is taken and appended to the sequence. Similarly, the process is repeated for all the cards picked by the player in the order that they pick the cards Let us assume that John has picked the following cards: Ace of Diamonds, 5 of Hearts, Ten of Spades, Queen of Clubs and the 6 of Hearts in the same order as specified. Therefore the sequence generated by John is as follows: DAHS STCQH6 Each player picks a maximum of 10 cards from which they can create their sequence. Once all the players have picked their cards, Mr X chooses his sequence of cards (without any knowledge of the cards picked by the players), which is going to be the Golden Sequence of cards. Mr. X can choose any number of cards less than or equal to 10. Let us assume that Mr X picks the following cards. Ace of Diamonds, 4 of Hearts, Ten of Spades, 8 of Hearts and 6 of Clubs. So the Golden Sequence is as follows: DAH4STH8C6 Once the Golden Sequence is found, a Likeness Score between the sequences of the players and the Golden Sequence is found. And finally, the player with the highest Likeness Score is declared the winner. Rules for Likeness Score: While finding the Likeness Score, more priority is given to the Suit of the cards rather than the Rank of the card. Rules include: First, the number of cards under consideration in the player's sequence and the Golden Sequence must be the same. So if the player has picked 10 cards, while the Golden Sequence has only 5 cards, then sub-sequences of 5 cards from the original sequence must be obtained. Something like this: Player's Sub-Sequences to be considered Golden Sequence HAD 2 S3C4H5D6S7C8H9CT HAD2s3C4H5D6S7C8H9CT HAD2S3C4H5D6S7C8H9CT H6C8SJDKS3 HAD2s3C4H5D6S7C8H9CT HAD2s3C4H5D6S7C8H9CT HAD2s3C4H5D6S7C8H9CT When the two sequences to be considered are available, The suit of the first card in both sequences are taken into account. If the suit is the same, then we keep track of those positions where the suit of the card is the same Next, if and only if the suit of the cards under consideration is the same, we look at the rank of the card. If the rank of the cards are also the same, a bonus point of 1 (for every such match) is added in the calculation of the Likeness Score. o Finally, once all the cards have been compared, the overall Likeness Score is calculated as follows: Likeness Score = ( Number of Cards where the suit is same / Number of Cards ) + ( 1 * Number of Cards with Same Suit and Same Rank) Example: Let us look at John's sequence and the Golden Sequence Cards #1 #2 #3 #4 #5 Player Sequence/Sub-Sequence D A H 5 STCO H6 IT +1 X X Golden Sequence D A H 4 S T H 8 C 6 +1 Not Considered as suit is different; leading to no bonus although rank is same Not Considered as suit is different; leading to no bonus Considered; +1 bonus added as suit and rank are same Considered; no bonus although same suit Therefore: 3 Likeness Score = 5 +2 = 2.6 Thus, the Range of the Likeness Scores is: [0, 1 + Number of Cards in Sequences] In this project (Questions 4-7) you will be creating an interactive program in C++ to allow users to play this game by implementing the following features: Q4: calcLikenessscore() - A function to calculate the likeness between two sequences of equal length Q5: bestLitenessscore () - A function to calculate the best Likeness Score among all the sub-sequences in a sequence and a given Golden Sequence Q6: findWinner() - A function to find the winner among 3 players whose sequence has the best Likeness Score with the Golden Sequence. Q7: Putting it All Together - Write a main() function that is going to call all the three functions created above to make the players play the game. You're welcome to write additional helper functions as you need. Write your code and test each function on your VS Code. Then, once finished, you can submit it on Canvas coderunner to make sure it's fully functional. All the functions and the main function should be in one file, SequenceOfCards.cpp Question 5: bestLikenessScore () (8 points) Write a function called bestLikenessscore () that is going to find the best Likeness Score between all the subsequences of a sequence (whose length is greater than or equal to the Golden Sequence) and the Golden Sequence. This function finds the maximum possible score a player could have. Function Specifications: Name: bestLikenessscore () Parameters (Please Follow the same Order): o seqi (string) - The Player's Sequence (length greater than or equal to Golden Sequence) o gold_seg (string) - The Golden Sequence Return Value: Best Likeness Score - best_likeness_score (double) Length of seqi should be greater than or equal to gold_seg for the function to calculate the Best Likeness Score. If not, return -1. Compare the sub-sequences from the player's sequence to the Golden Sequence to find the Best Likeness Score among all the sub-sequences. Use the previous calcLikenessscore () function from Question 4 to find the Likeness Score once the sub-sequence is obtained. The function should not print anything. Example: Expected output from a Longer Player's Sequence and the Golden Sequence segi seg2 likeness_score S7H8SJD 9HXCJD9 0 S7H8SJD 9H8CJD9 1.67 S7H8SJD 9H8CJD9 H8C6D6 0 S7H8SJD 9H8CJD9 0 S7H8SJD 9H8CJD9 2. 2 The function should calculate the Likeness Score between all the sub-sequences and the Golden Sequence and should return only the Best Likeness Score as indicated. In the example above, the last subsequence has the highest score, 2, and therefore 2 should be the return value. The file should be named as bestLikenessScore.cpp. Once you have tested your code on VS Code, then head over to coderunner on Canvas and paste only your function in the answer box! DECK OF CARDS The standard 52-card deck of French-suited playing cards is the most common pack of playing cards used today. A standard 52-card pack comprises 13 ranks in each of the four French suits: Clubs (6), Diamonds (), Hearts () and Spades (), with reversible (double-headed) court cards (face cards). Each suit includes an Ace, a King, Queen and Jack, each depicted alongside a symbol of its suit; and numerals or pip cards from the Deuce (Two) to the Ten, with each card depicting that many symbols (pips) of its suit. Example set of 52 playing cards; 13 of each suit: clubs, diamonds, hearts, and spades 2 3 4 5 6 7 8 9 10 Jack Queen King Ace Clubs : Diamonds . . Hearts E Spades Ref: Standard 52-Card Deck SEQUENCE OF CARDS John, Mike and Suzy head to the Carnival at Zootopia. They come across a stall named "Can You Pick 'em Right?!. The stall owner Mr X greets them and invites them to play his game and tells them that the winner will get a coupon worth $50 to spend in the Carnival. The three friends get excited and decide to play the game. Mr X starts to explain the game to the participants. The ultimate aim of the game is for the players to create a sequence by picking a set of cards which is similar to the sequence picked by the host, i.e., Mr X. He says that every player is free to choose up to a maximum of 10 cards to form their sequence. A sequence is formed by the cards picked by the players. The players select a subsequence of cards from their hand to compare against the golden sequence. The players cannot rearrange the cards, but can select a continuous subset that is the same length as the golden sequence. The game is played with multiple decks of cards. We know that in a deck of cards there are four suits: Spades (S), Hearts (H), Diamonds (D) and Clubs (C). And there are 13 ranks in each suit: Ace, 2-10, Jack, Queen and King. For the purpose of creating the sequence Ace is treated as the character A, Ten as T, Jack as J, Queen as Q and King as K. Formation of Sequences: First, the card's suit is taken and the letter representing that suit is added to the sequence. Next, the card's rank is taken and appended to the sequence. Similarly, the process is repeated for all the cards picked by the player in the order that they pick the cards Let us assume that John has picked the following cards: Ace of Diamonds, 5 of Hearts, Ten of Spades, Queen of Clubs and the 6 of Hearts in the same order as specified. Therefore the sequence generated by John is as follows: DAHS STCQH6 Each player picks a maximum of 10 cards from which they can create their sequence. Once all the players have picked their cards, Mr X chooses his sequence of cards (without any knowledge of the cards picked by the players), which is going to be the Golden Sequence of cards. Mr. X can choose any number of cards less than or equal to 10. Let us assume that Mr X picks the following cards. Ace of Diamonds, 4 of Hearts, Ten of Spades, 8 of Hearts and 6 of Clubs. So the Golden Sequence is as follows: DAH4STH8C6 Once the Golden Sequence is found, a Likeness Score between the sequences of the players and the Golden Sequence is found. And finally, the player with the highest Likeness Score is declared the winner. Rules for Likeness Score: While finding the Likeness Score, more priority is given to the Suit of the cards rather than the Rank of the card. Rules include: First, the number of cards under consideration in the player's sequence and the Golden Sequence must be the same. So if the player has picked 10 cards, while the Golden Sequence has only 5 cards, then sub-sequences of 5 cards from the original sequence must be obtained. Something like this: Player's Sub-Sequences to be considered Golden Sequence HAD 2 S3C4H5D6S7C8H9CT HAD2s3C4H5D6S7C8H9CT HAD2S3C4H5D6S7C8H9CT H6C8SJDKS3 HAD2s3C4H5D6S7C8H9CT HAD2s3C4H5D6S7C8H9CT HAD2s3C4H5D6S7C8H9CT When the two sequences to be considered are available, The suit of the first card in both sequences are taken into account. If the suit is the same, then we keep track of those positions where the suit of the card is the same Next, if and only if the suit of the cards under consideration is the same, we look at the rank of the card. If the rank of the cards are also the same, a bonus point of 1 (for every such match) is added in the calculation of the Likeness Score. o Finally, once all the cards have been compared, the overall Likeness Score is calculated as follows: Likeness Score = ( Number of Cards where the suit is same / Number of Cards ) + ( 1 * Number of Cards with Same Suit and Same Rank) Example: Let us look at John's sequence and the Golden Sequence Cards #1 #2 #3 #4 #5 Player Sequence/Sub-Sequence D A H 5 STCO H6 IT +1 X X Golden Sequence D A H 4 S T H 8 C 6 +1 Not Considered as suit is different; leading to no bonus although rank is same Not Considered as suit is different; leading to no bonus Considered; +1 bonus added as suit and rank are same Considered; no bonus although same suit Therefore: 3 Likeness Score = 5 +2 = 2.6 Thus, the Range of the Likeness Scores is: [0, 1 + Number of Cards in Sequences] In this project (Questions 4-7) you will be creating an interactive program in C++ to allow users to play this game by implementing the following features: Q4: calcLikenessscore() - A function to calculate the likeness between two sequences of equal length Q5: bestLitenessscore () - A function to calculate the best Likeness Score among all the sub-sequences in a sequence and a given Golden Sequence Q6: findWinner() - A function to find the winner among 3 players whose sequence has the best Likeness Score with the Golden Sequence. Q7: Putting it All Together - Write a main() function that is going to call all the three functions created above to make the players play the game. You're welcome to write additional helper functions as you need. Write your code and test each function on your VS Code. Then, once finished, you can submit it on Canvas coderunner to make sure it's fully functional. All the functions and the main function should be in one file, SequenceOfCards.cpp