The table used for the Question:

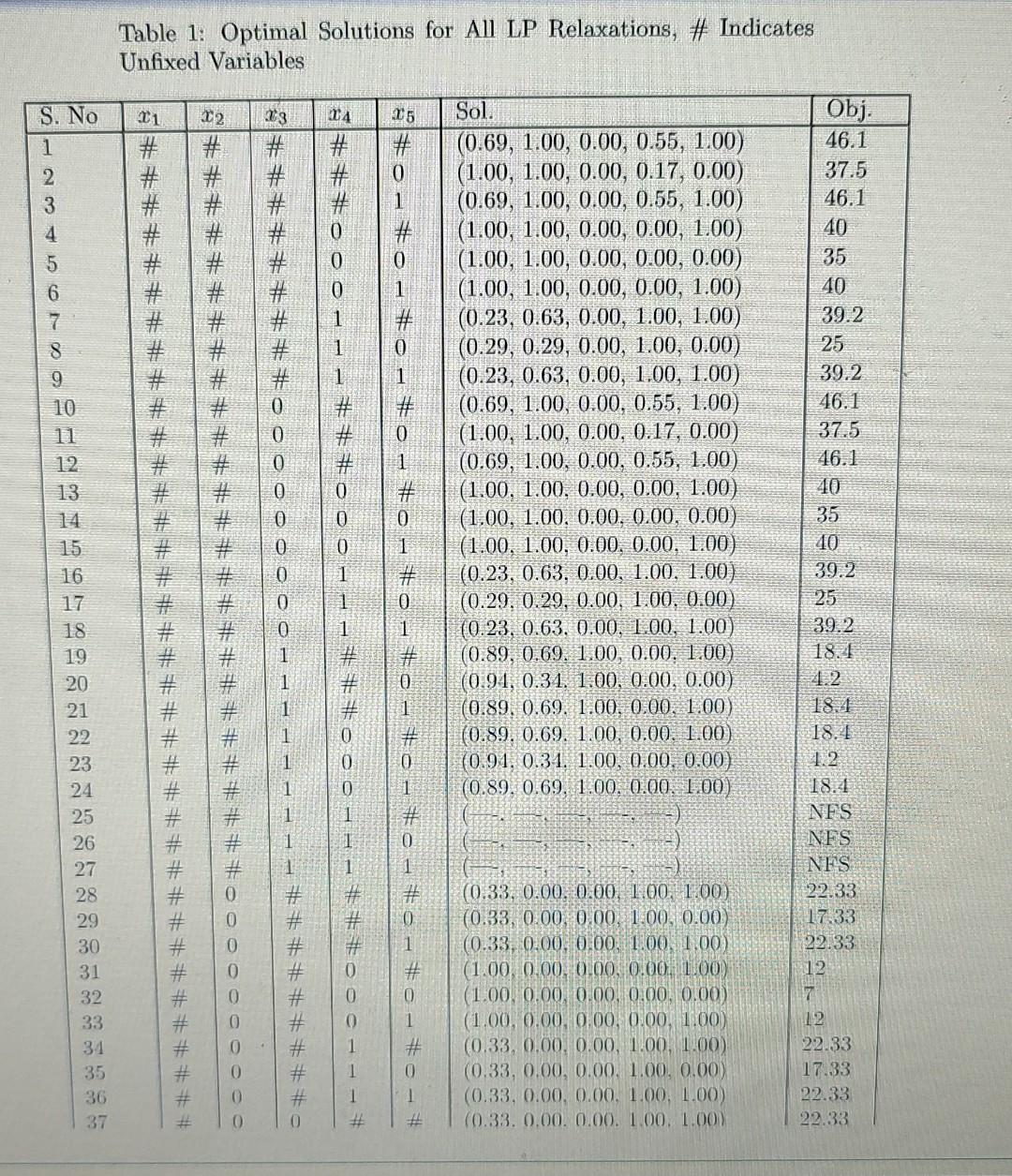
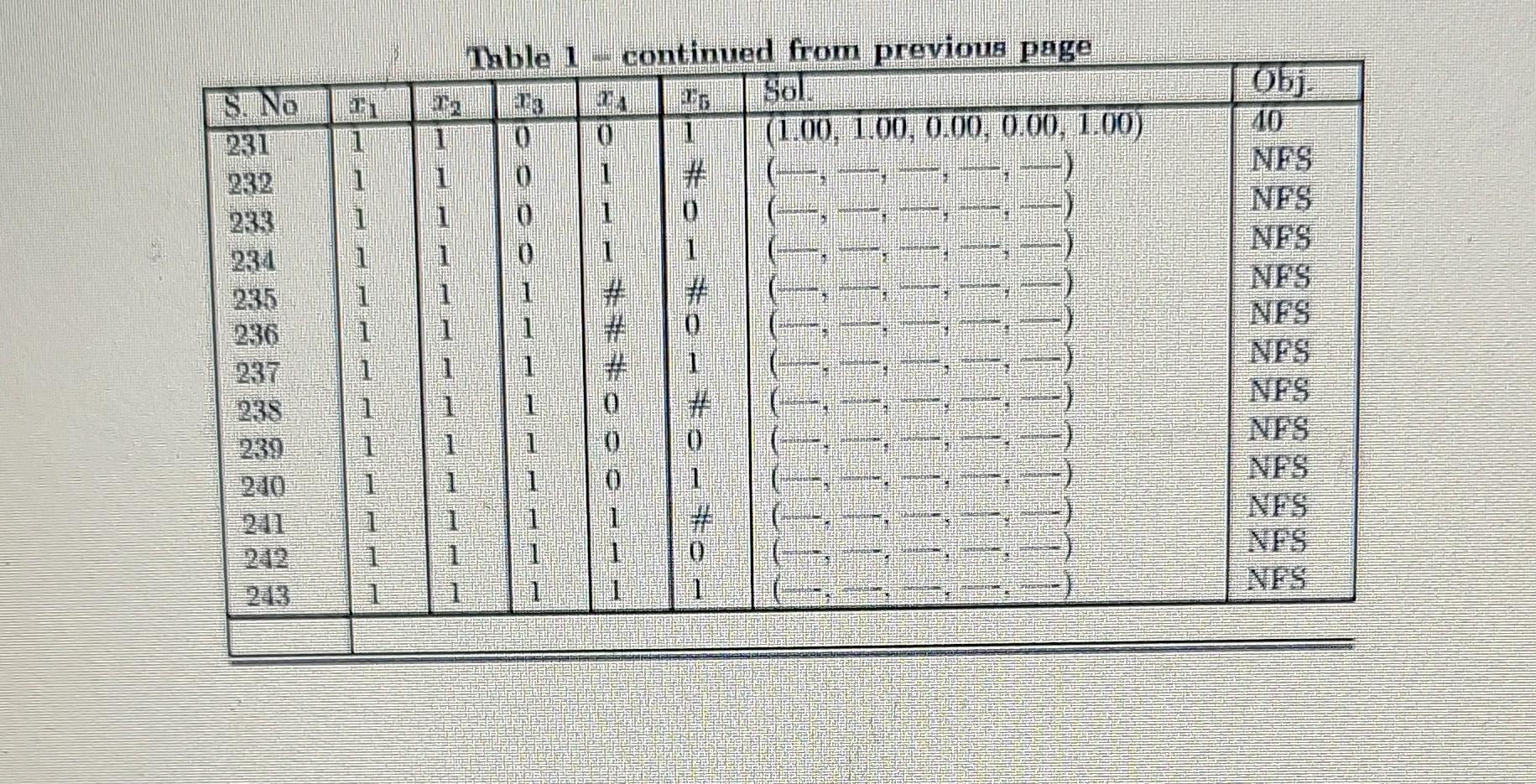
Consider the following IP problem. maximize : 7x1+28x212x3+15x4+5x5subbjertto:50x170x2+40x3+30x430x510010x1+60x2+50x3+60x420x5806x1+1x2+3x3+7x49xi{0,1}i=1,,5 (a) Write the LP relaxation of the above model. (b) Get the optimal objective function value of the LP relaxation from Table 1. Is it a lower or an upper bound? Explain. (c) Is x=[1,0,0,0,1)T a feasible solution to the above problem. If yes, then obtain its objective function value from Table 1. Is it a lower or an upper bound? Explain. Solve the above problem using branch \& bound method, and build the entmeration tree using thie following strategies. You can use the information from Table 1. Nole: Generate ome tree for Pert (d). one for Pat (c) and one for Part (f). Drinu insule eret node. the node namber Neezt to the tree. you should fatlow the strategies as deseribed. Burting the euterition of aimy stralegy. if Report the incumbent solution. Also, suy in peris itage. liom far is is fimm thi best possible selutionm For Strategy-1, write the BP formutation that uras. solved at every nit node. (d) Strategy-1: - Node Selection: Best First Select the node with the best objective function value: - Variable Selection: Nearest to integer A fractional variable with fractional valug nenest to antinteger will be used for branching. - Branching Direction: Up Select the branch of side (lower hound is incrensed.) (e) Strategy-2: - Node Selection: Depth First the Best Back Select the most recently created child node to solve. If no child exists, then backtrack to the best bound node available in the entire tree. - Variable Selection: Lowest fraction A fractional variable with lowest fraction will be used for branching. - Branching Direction: Down Select the branch of side (upper bound is decreased.) (f) Strategy-3: - Node Selection: Breadth First the Best Next All nodes at one level of the search tree are processed before any node at a deeper level. In a given level, best node should be processed first. - Variable Selection: Highest fraction A fractional variable with highest fraction will be used for branching. - Branching Direction: You are free to pick eny rule. ISE-321 HW-2 Table 1: Optimal Solutions for All LP Relaxations, \# Indicates Unfixed Variables Table 1: Optimal Solutions for All LP Relaxations, \# Indicates Table 1 - continued from previous page Consider the following IP problem. maximize : 7x1+28x212x3+15x4+5x5subbjertto:50x170x2+40x3+30x430x510010x1+60x2+50x3+60x420x5806x1+1x2+3x3+7x49xi{0,1}i=1,,5 (a) Write the LP relaxation of the above model. (b) Get the optimal objective function value of the LP relaxation from Table 1. Is it a lower or an upper bound? Explain. (c) Is x=[1,0,0,0,1)T a feasible solution to the above problem. If yes, then obtain its objective function value from Table 1. Is it a lower or an upper bound? Explain. Solve the above problem using branch \& bound method, and build the entmeration tree using thie following strategies. You can use the information from Table 1. Nole: Generate ome tree for Pert (d). one for Pat (c) and one for Part (f). Drinu insule eret node. the node namber Neezt to the tree. you should fatlow the strategies as deseribed. Burting the euterition of aimy stralegy. if Report the incumbent solution. Also, suy in peris itage. liom far is is fimm thi best possible selutionm For Strategy-1, write the BP formutation that uras. solved at every nit node. (d) Strategy-1: - Node Selection: Best First Select the node with the best objective function value: - Variable Selection: Nearest to integer A fractional variable with fractional valug nenest to antinteger will be used for branching. - Branching Direction: Up Select the branch of side (lower hound is incrensed.) (e) Strategy-2: - Node Selection: Depth First the Best Back Select the most recently created child node to solve. If no child exists, then backtrack to the best bound node available in the entire tree. - Variable Selection: Lowest fraction A fractional variable with lowest fraction will be used for branching. - Branching Direction: Down Select the branch of side (upper bound is decreased.) (f) Strategy-3: - Node Selection: Breadth First the Best Next All nodes at one level of the search tree are processed before any node at a deeper level. In a given level, best node should be processed first. - Variable Selection: Highest fraction A fractional variable with highest fraction will be used for branching. - Branching Direction: You are free to pick eny rule. ISE-321 HW-2 Table 1: Optimal Solutions for All LP Relaxations, \# Indicates Unfixed Variables Table 1: Optimal Solutions for All LP Relaxations, \# Indicates Table 1 - continued from previous page