Answered step by step
Verified Expert Solution
Question
1 Approved Answer
This information is also given for help Figure 1.1 contains a schematic of a fluid flowing between two parallel plates with an applied pressure gradient

This information is also given for help





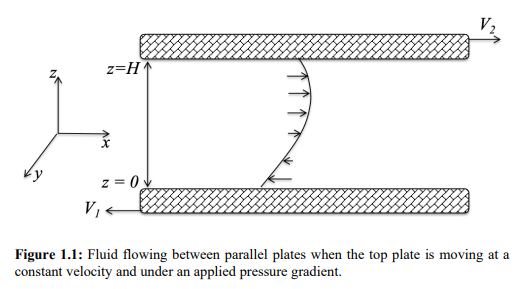
 Figure 1.1 contains a schematic of a fluid flowing between two parallel plates with an applied pressure gradient (dp/dx) considered to be a constant. The top plate and bottom plate are being moved at velocities equal to V2 and V1, respectively. The separation between the two plates is defined as H. Note that the velocity profile shown in the Figure 1.1 schematic is hypothetical. The viscosity of the fluid is defined as . Answer all the questions below. State all assumptions and show all work. a) Determine the velocity profile vx in terms of (dp/dx),V1,V2,,H, and the dimensionless coordinate =z/H. b) If V1=0, the velocity profile is vx=1dxdp2H2[2]+V2 Determine the pressure gradient (dp/dx), which is required to reduce the volumetric flowrate of the fluid to 0 . The answer should be expressed in terms of V2,, and H. c) For the condition when the volumetric flowrate is zero, at what value of does the velocity exhibit a maximum when the fluid is flowing in the negative x-direction? d) Provide a sketch of the velocity profile when the volumetric flowrate is zero on a schematic similar to the one shown in Figure 1.1. Make sure to label the sketch as much as possible and indicate where the velocity is equal to zero or the location of any maxima or minima. Figure 1.1: Fluid flowing between parallel plates when the top plate is moving at a constant velocity and under an applied pressure gradient. Components of the stress tensor for a Newtonian fluid in spherical coordinates rr=[2rvr32(v)]=[2(r1v+rvr)32(v)]=[2(rsin1v+rvr+rvcot)32(v)]r==[rr(rv)+r1vr]==[rsin(sinv)+rsin1v]=r=[rsin1vr+rr(rv)] Components of the stress tensor for a Newtonian fluid in cylindrical coordinates rr=[2rvr32(v)]=[2(r1v+rvr)32(v)]zz=[2zvz32(v)]r=r=[rr(rv)+r1vr]z=z=[zv+r1vz]zr=rz=[rvz+zvr] Components of the stress tensor for a Newtonian fluid in rectangular coordinates xx=[2xvx32(v)]yy=[2yvy32(v)]zz=[2zvz32(v)]xy=yx=[yvx+xvy]yz=zy=[zvy+yvz]zx=xz=[xvz+zvx] Equation of motion in spherical coordinates for a Newtonian fluid with constant and . r-component (tvr+vrrvr+rvvr+rsinvvrrv2+v2)=rp+[r21r22(r2vr)+r2sin1(sinvr)+r2sin2122vr]+gr -component (tv+vrrv+rvv+rsinvv+rvrvrv2cot)=r1p+[r21r(r2rv)+r21(sin1(vsin))+r2sin2122v+r22vrr2sin22cosv]+g -component (tv+vrrv+rvv+rsinvv+rvvr+rvvcot)=rsin1p+[r21r(r2rv)+r21(sin1(vsin))+r2sin2122v+r2sin2vr+r2sin22cosv]+g Equation of motion in cylindrical coordinates for a Newtonian fluid with constant and . r-component (tvr+vrrvr+rvvrrv2+vzzvr)=rp+[r(r1r(rvr))+r2122vrr22v+z22vr]+gr -component (tv+vrrv+rvv+rvrv+vzzv)=r1p+[r(r1r(rv))+r2122v+r22vr+z22v]+gz-component(tvz+vrrvz+rvvz+vzzvz)=zp+[r1r(rrvz)+r2122vz+z22vz]+gz Equation of motion in rectangular coordinates for a Newtonian fluid with constant and : x-component (tvx+vxxvx+vyyvx+vzzvx)=xp+(x22vx+y22vx+z22vx)+gx y-component (tvy+vxxvy+vyyvy+vzzvy)=yp+(x22vy+y22vy+z22vy)+gy z-component (tvz+vxxvz+vyyvz+vzzvz)=zp+(x22vz+y22vz+z22vz)+gz
Figure 1.1 contains a schematic of a fluid flowing between two parallel plates with an applied pressure gradient (dp/dx) considered to be a constant. The top plate and bottom plate are being moved at velocities equal to V2 and V1, respectively. The separation between the two plates is defined as H. Note that the velocity profile shown in the Figure 1.1 schematic is hypothetical. The viscosity of the fluid is defined as . Answer all the questions below. State all assumptions and show all work. a) Determine the velocity profile vx in terms of (dp/dx),V1,V2,,H, and the dimensionless coordinate =z/H. b) If V1=0, the velocity profile is vx=1dxdp2H2[2]+V2 Determine the pressure gradient (dp/dx), which is required to reduce the volumetric flowrate of the fluid to 0 . The answer should be expressed in terms of V2,, and H. c) For the condition when the volumetric flowrate is zero, at what value of does the velocity exhibit a maximum when the fluid is flowing in the negative x-direction? d) Provide a sketch of the velocity profile when the volumetric flowrate is zero on a schematic similar to the one shown in Figure 1.1. Make sure to label the sketch as much as possible and indicate where the velocity is equal to zero or the location of any maxima or minima. Figure 1.1: Fluid flowing between parallel plates when the top plate is moving at a constant velocity and under an applied pressure gradient. Components of the stress tensor for a Newtonian fluid in spherical coordinates rr=[2rvr32(v)]=[2(r1v+rvr)32(v)]=[2(rsin1v+rvr+rvcot)32(v)]r==[rr(rv)+r1vr]==[rsin(sinv)+rsin1v]=r=[rsin1vr+rr(rv)] Components of the stress tensor for a Newtonian fluid in cylindrical coordinates rr=[2rvr32(v)]=[2(r1v+rvr)32(v)]zz=[2zvz32(v)]r=r=[rr(rv)+r1vr]z=z=[zv+r1vz]zr=rz=[rvz+zvr] Components of the stress tensor for a Newtonian fluid in rectangular coordinates xx=[2xvx32(v)]yy=[2yvy32(v)]zz=[2zvz32(v)]xy=yx=[yvx+xvy]yz=zy=[zvy+yvz]zx=xz=[xvz+zvx] Equation of motion in spherical coordinates for a Newtonian fluid with constant and . r-component (tvr+vrrvr+rvvr+rsinvvrrv2+v2)=rp+[r21r22(r2vr)+r2sin1(sinvr)+r2sin2122vr]+gr -component (tv+vrrv+rvv+rsinvv+rvrvrv2cot)=r1p+[r21r(r2rv)+r21(sin1(vsin))+r2sin2122v+r22vrr2sin22cosv]+g -component (tv+vrrv+rvv+rsinvv+rvvr+rvvcot)=rsin1p+[r21r(r2rv)+r21(sin1(vsin))+r2sin2122v+r2sin2vr+r2sin22cosv]+g Equation of motion in cylindrical coordinates for a Newtonian fluid with constant and . r-component (tvr+vrrvr+rvvrrv2+vzzvr)=rp+[r(r1r(rvr))+r2122vrr22v+z22vr]+gr -component (tv+vrrv+rvv+rvrv+vzzv)=r1p+[r(r1r(rv))+r2122v+r22vr+z22v]+gz-component(tvz+vrrvz+rvvz+vzzvz)=zp+[r1r(rrvz)+r2122vz+z22vz]+gz Equation of motion in rectangular coordinates for a Newtonian fluid with constant and : x-component (tvx+vxxvx+vyyvx+vzzvx)=xp+(x22vx+y22vx+z22vx)+gx y-component (tvy+vxxvy+vyyvy+vzzvy)=yp+(x22vy+y22vy+z22vy)+gy z-component (tvz+vxxvz+vyyvz+vzzvz)=zp+(x22vz+y22vz+z22vz)+gz Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


