Answered step by step
Verified Expert Solution
Question
1 Approved Answer
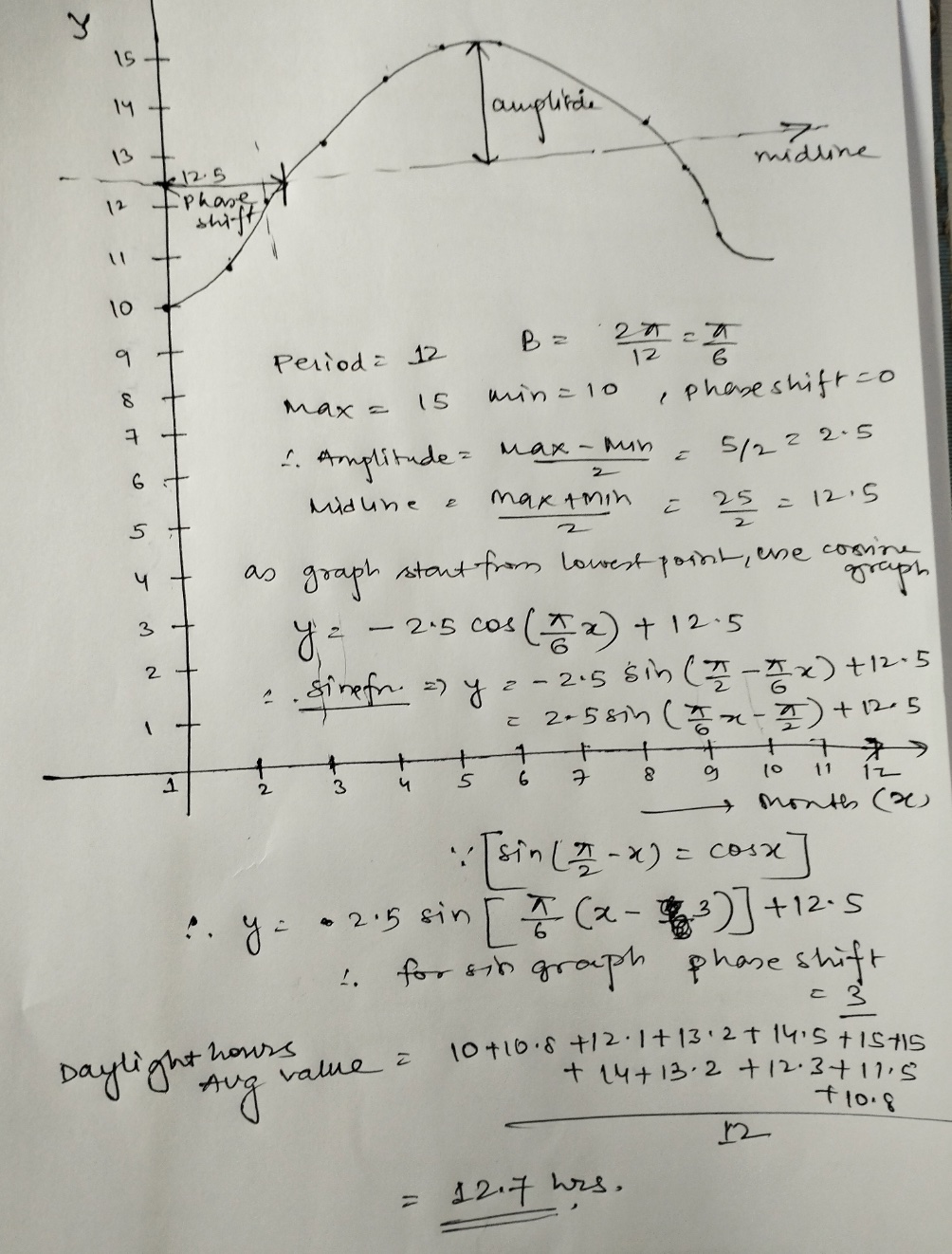
Use a graphing calculator or technology to perform sinusoidal regression that will determine the sine function that best fits the data. Record the equation. Choose
- Use a graphing calculator or technology to perform sinusoidal regression that will determine the sine function that best fits the data. Record the equation.
- Choose a temperature (not a max or min temperature) and use the equation from part a) to find the months when the temperature is above your chosen temperature.
- Choose a month when the temperature is changing at a negative rate. Determine the instantaneous rate of change of temperature at that point.
SAMPLE:
- All sunrise and sunset data are taken from the first day of each month.
- All times have been converted to hours using decimal values: i.e. 5 hr 45 min = 5 + 45/60 = 5.75 hrs.
- Daylight hours are the difference between sunset time and sunrise time.
- Temperature is the average monthly temperature.
- DATA:
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


