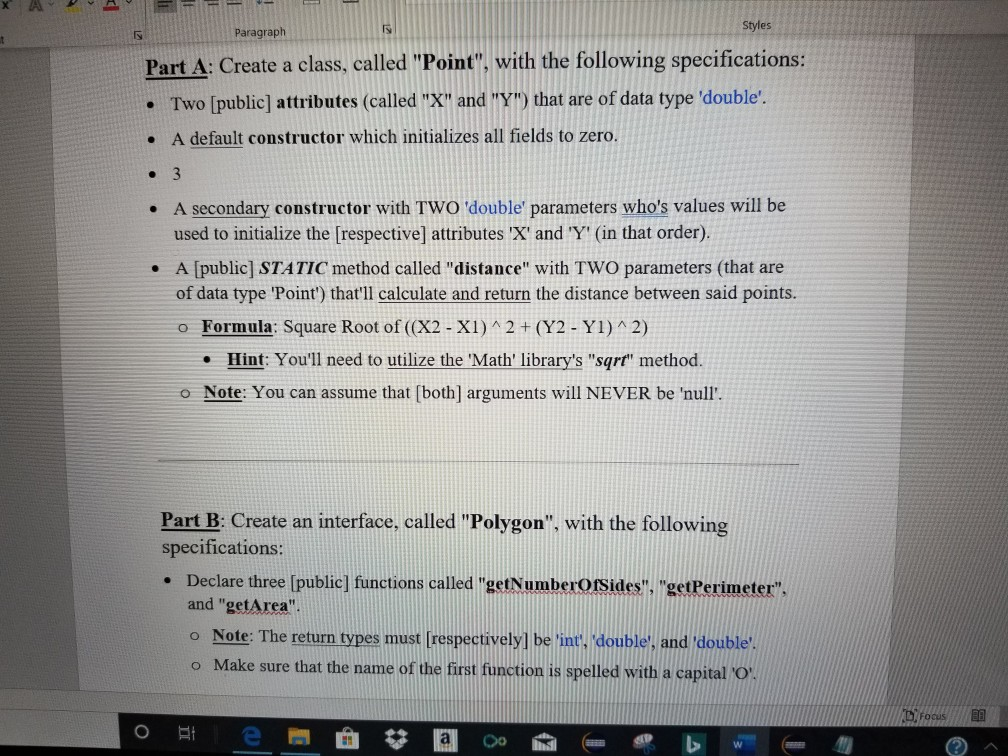
use of just Java

Part A: Create a class, called "Point", with the following specifications: Two (public) attributes (called "X" and "Y") that are of data type 'double'. A default constructor which initializes all fields to zero. 3 A secondary constructor with TWO 'double' parameters who's values will be used to initialize the respective] attributes 'X' and 'Y' (in that order). A public) STATIC method called "distance" with TWO parameters that are of data type 'Point') that'll calculate and return the distance between said points. o Formula: Square Root of ((X2 - X1)^2 + (Y2 - Y1)^2) Hint: You'll need to utilize the 'Math' library's "sort" method. o Note: You can assume that [both] arguments will NEVER be 'null'. Part B: Create an interface, called "Polygon", with the following specifications: Declare three [public) functions called "getNumberOfSides", "getPerimeter", and "getArea". o Note: The return types must respectivelyl be 'int', 'double', and 'double'. A = Styles Paragraph Part A: Create a class, called "Point", with the following specifications: Two (public) attributes (called "X" and "Y") that are of data type 'double'. A default constructor which initializes all fields to zero. 3 A secondary constructor with TWO 'double' parameters who's values will be used to initialize the [respective) attributes 'X' and 'Y' (in that order). A [public] STATIC method called "distance" with TWO parameters (that are of data type 'Point') that'll calculate and return the distance between said points. o Formula: Square Root of ((X2 - X1)^2 + (Y2 - Y1)^2) Hint: You'll need to utilize the 'Math' library's "sqrt" method. Note: You can assume that [both] arguments will NEVER be 'null'. Part B: Create an interface, called "Polygon", with the following specifications: Declare three (public] functions called "getNumberOfSides", "getPerimeter". and "getArea" o Note: The return types must [respectivelyl be 'int', 'double', and double!! o Make sure that the name of the first function is spelled with a capital 'O'. Focus 38 o e a corpo W styles Paragraph Part C: Create an ABSTRACT class, called "Simple Polygon" (which implements our 'Polygon' interface) with the following specifications: A protected attribute that's an array of 'Point's, called "vertices". o Important: For the following class and remaining parts), how the elements are organized does matter, HOWEVER, to make things more manageable, you can assume that all of this array's points will always) be organized in a clockwise manner. For examples: . (0, 1) => (1, 1) => (1, 0) > (0,0) forms a 'square', where as .. . (0, 1) => (1, 0) > (0,0) => (1, 1) would form a 'hourglass'. As seen with the latter example, if lines were drawn between [adjacent) points, then we'd have intersecting edges. You can assume that said scenarios will NEVER occur. A constructor, with ONE integer parameter, that'll define the 'vertices' attribute with a new array of 'Point's (where it's size is based on said parameter's value). o Important: If argument is less than 3, throw a 'IllegalArgumentException! o Note: No other constructors should be present (even the default constructor). Implement the [inherited] "getNumberOfSides" function. Hint: There's a [direct] correlation between the number of edges and points. Define a [public) function called "isEquilateral" which will return true if all of this polygon's sides are of equal length (otherwise it'll return false). o Important: This should go without saying, but make sure that this function works no matter how many sides / vertices there are. Focus - o e a coa - SP * AD AdBbc AaBb Emphasis Heading 1 99 AaBbCel. AaBbCd AaBbcc AaBb Normal Strong Subtitle Title AaBbcc Aabbcc 1 No Spac... Subtle Em... Paragraph Styles Part D: Create a class called "Triangle", which extends from our Simple Polygon' class, with the following specifications: A constructor with THREE parameters that are all of data type 'Point'. The given values must then be assigned into the 'vertices' array (in order). o Hint: Don't forget to invoke the superclass' constructor (using the 'super' Keyword and an appropriate value). o Note: You can assume that [all] arguments will be "non-null" values. Implement the inherited] "getPerimeter" function. o As the name implies, this function should return the total (sum) length between this class' [3] vertices ("A => B", "B => C" and "C => A"). Tip: Again, invoke class 'Point's distance function. Implement the [inherited] "getArea" function. o As the name implies, this function should return the area that this class' [31 vertices surround. This can be easily found using the following equation: Legend: Vertex 1 = (x1, yl), Vertex 2 = (x2, y2), Vertex 3 = (x3, y3) Formula: Absolute value of ((x1 * (y2 - y3) + x2 * (y3 - yl) + x3 + (y1 - y2))/2) L Focus AO-A Emphasis Heading Normal Strong Strong Subtitle Title No Spact Subtle Em. Intense E... Paragraph Styles Part E: Create a class called "Quadrilateral", which extends from our Simple Polygon' class, with the following specifications: A constructor with FOUR parameters that are all of data type 'Point The given values must then be assigned into the 'vertices' array (in order). o Hint: Don't forget to invoke the superclass' constructor (using the 'super' keyword and an appropriate value). o Note: You can assume that [all] arguments will be "non-null" values. Implement the [inherited] "getPerimeter" function. o As the name implies, this function should return the total (sum) length between this class' vertices ("A => B", "B => C", "C => D" and "D=> A"). Tip: Again, invoke class 'Point's distance function. Implement the [inherited] "getArea" function. o As the name implies, this function should return the area that this class' vertices surround. This can be easily found using the following equation: . Legend Vertex 1 = A, Vertex 2 =B, Vertex 3 = C, Vertex 4 =D - Formula: (Area of Triangle 'ABD') + (Area of Triangle 'BCD') O Tip: Take advantage of our very own Triangle class. D. Focus 282 te