USING C++ LANGUAGE ONLY.
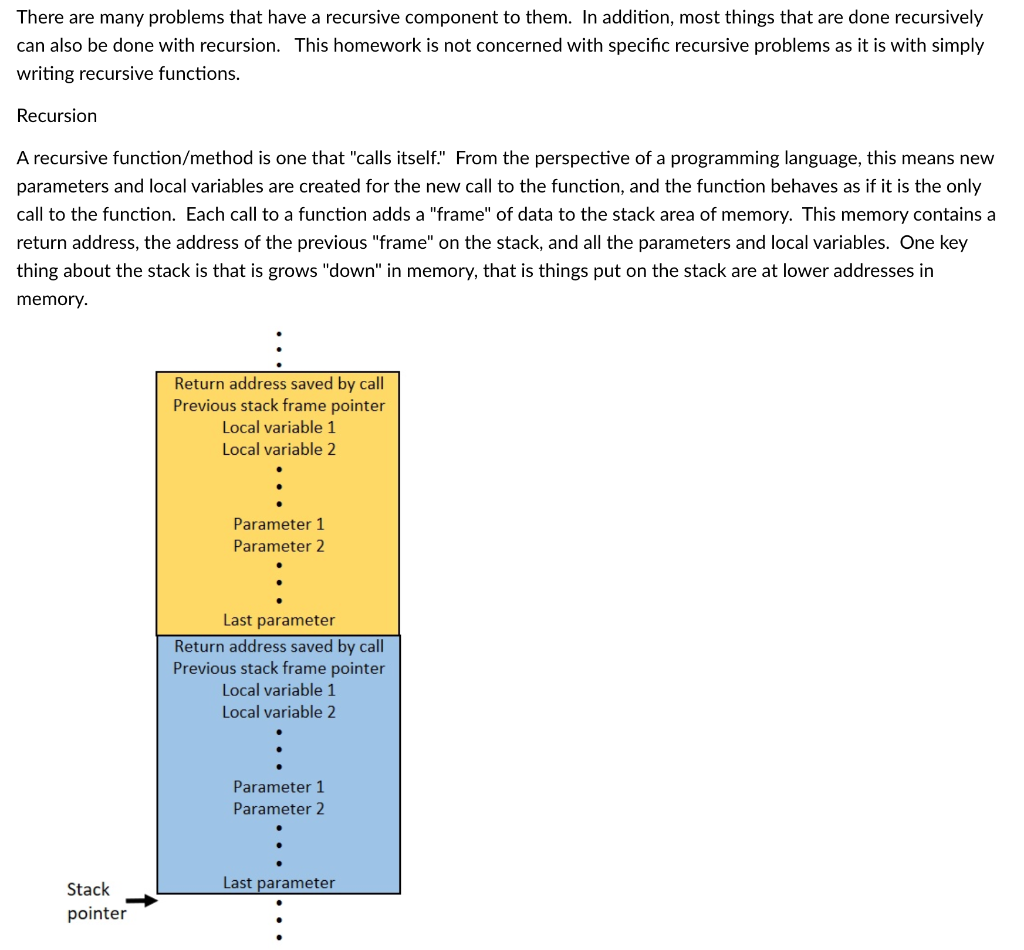

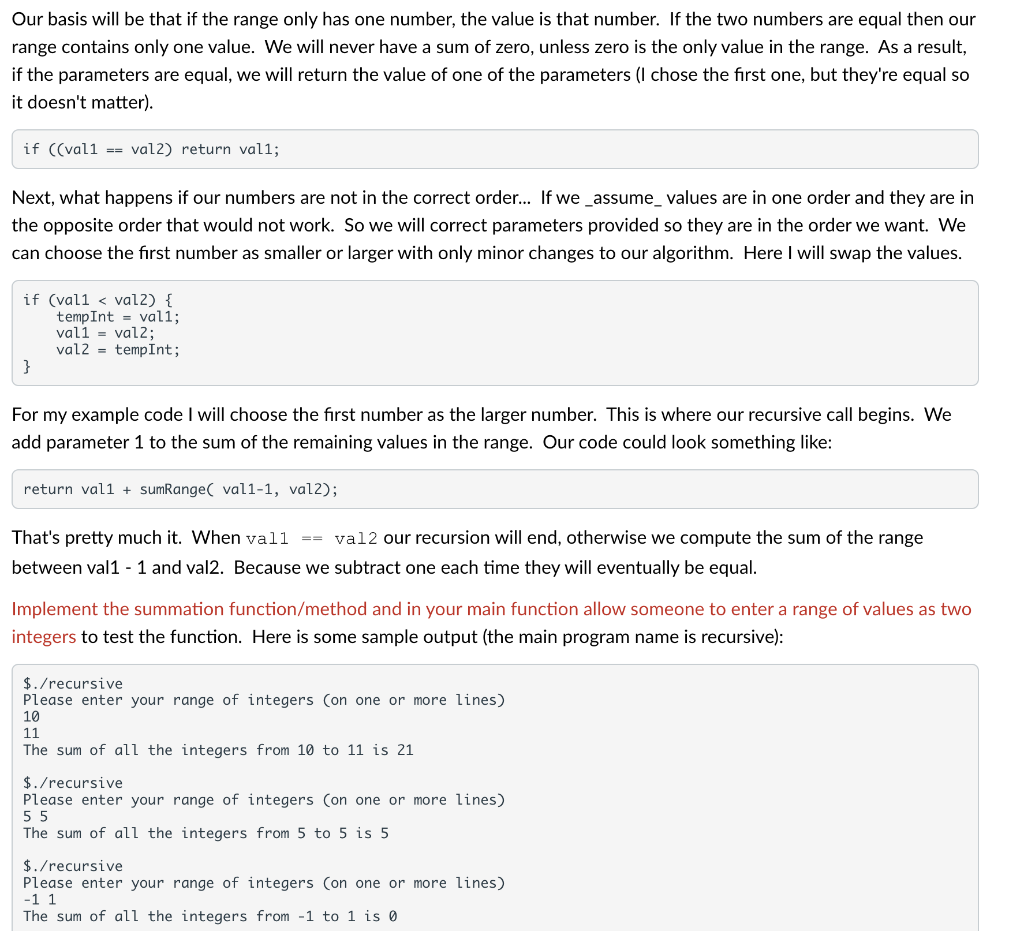
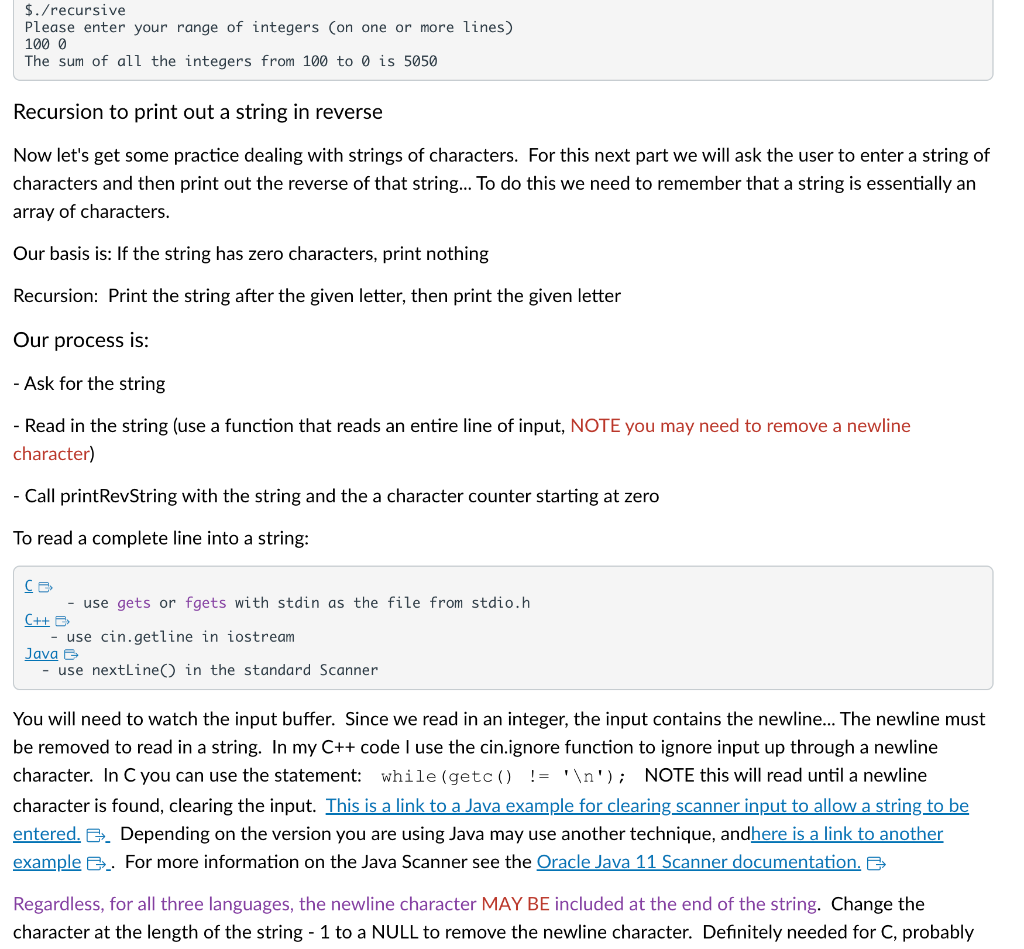
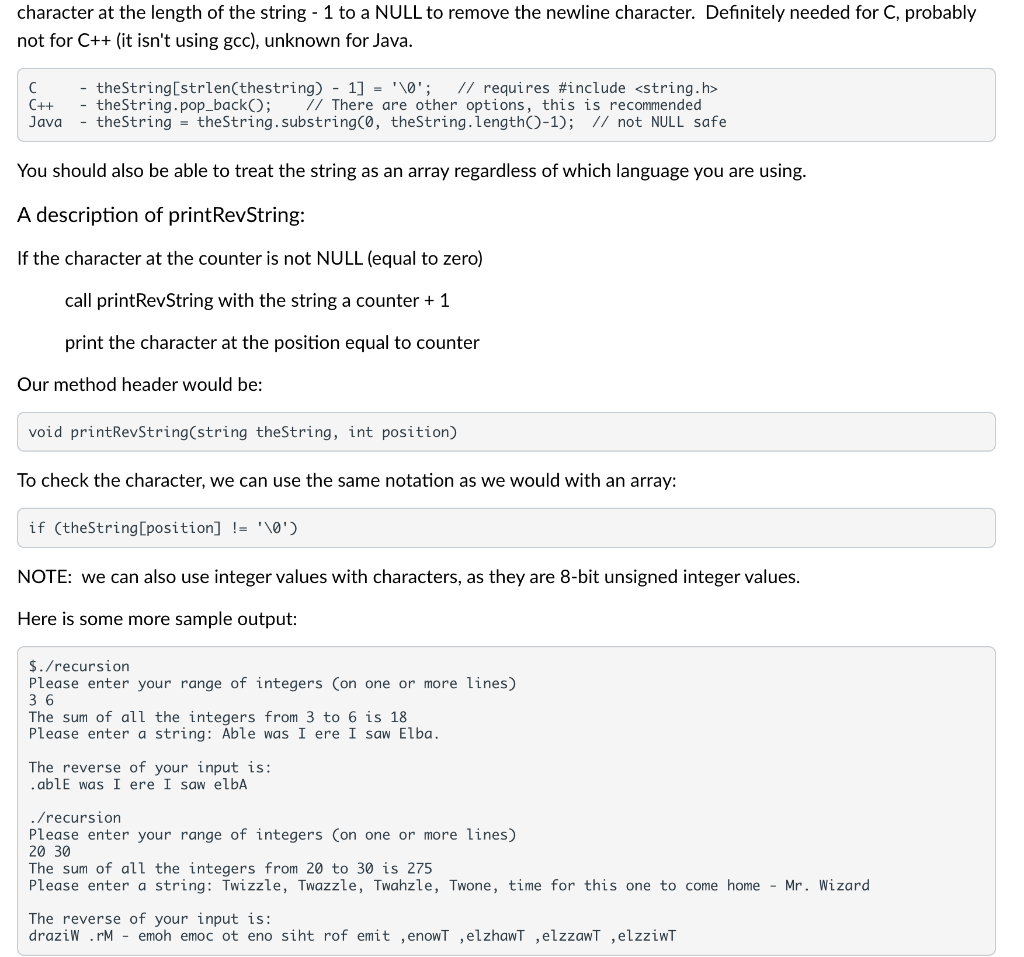
There are many problems that have a recursive component to them. In addition, most things that are done recursively can also be done with recursion. This homework is not concerned with specific recursive problems as it is with simply writing recursive functions. Recursion A recursive function/method is one that "calls itself." From the perspective of a programming language, this means new parameters and local variables are created for the new call to the function, and the function behaves as if it is the only call to the function. Each call to a function adds a "frame" of data to the stack area of memory. This memory contains a return address, the address of the previous "frame" on the stack, and all the parameters and local variables. One key thing about the stack is that is grows "down" in memory, that is things put on the stack are at lower addresses in memory. Because each call produces a new stack "frame" the memory locations for parameters and variables are different for each call, allowing us to have a function call itself without overwriting needed memory information. The two parts of recursion: Basis: when do we stop?? For most recursive functions and methods we view the basis as the stopping point. From a more general perspective, the basis is the start from which the solution is built. Also called the "base case", the basis is the part of the input to the recursion for which no recursive call is needed. For example, the Fibonacci sequence is recursively defined as follows: Basis: Fibonacci (1)=1, Fibonacci (2)=1 When we are trying to find the first or second Fibonacci number we do not make a recursive call. NOTE: Sometimes we define the basis as: F(0)=0 and F(1)=1, though the value at zero is not really defined. Numerically we get the same answers for all input values greater than 1. The "recursive step": The recursive step or part tells us how to build new values. Each recursive value is determined using one or more values that have been previously determined. With Fibonacci, the values for Fibonacci(1) and Fibonacci(2) are already determined by the basis., so we don't need a formula to tell us how to find them. All the other values are given by the formula: Fibonacci (n)= Fibonacci(n-1) + Fibonacci (n2) for integer n>2 This is the definition of recursion, in that the value of our function for some given inputs depends on the value of the function for "previous" inputs. Our first recursive function First, let's write a function to sum all the integers in the range between two integers. Algorithm design: We need a function that will take two parameters and return an integer. So we will have a header that looks something like: int sumRange(int val1, int val2) Our basis will be that if the range only has one number, the value is that number. If the two numbers are equal then our range contains only one value. We will never have a sum of zero, unless zero is the only value in the range. As a result, if the parameters are equal, we will return the value of one of the parameters ( ch chose the first one, but they're equal so it doesn't matter). if ((val1==val2) return val1; Next, what happens if our numbers are not in the correct order... If we_assume_values are in one order and they are in the opposite order that would not work. So we will correct parameters provided so they are in the order we want. We can choose the first number as smaller or larger with only minor changes to our algorithm. Here I will swap the values. if ( val 1











