Using the information about G2 above as an input to Dijkstra's algorithm, produce exactly the same kind of solution information for G2 as illustrated by parts one and two of the solution of the G1 example problem above.

Thus, you will execute Dijkstra's algorithm (by hand) on G2, you will find the lengths of all the shortest paths from node #1 in G2 to all the other nodes, and you will find the shortest paths themselves.

Note: The important thing here is that you get as close to possible to creating the output information correctly by using the adjacency matrix information. It's a way to show your understanding of the details of the algorithm.

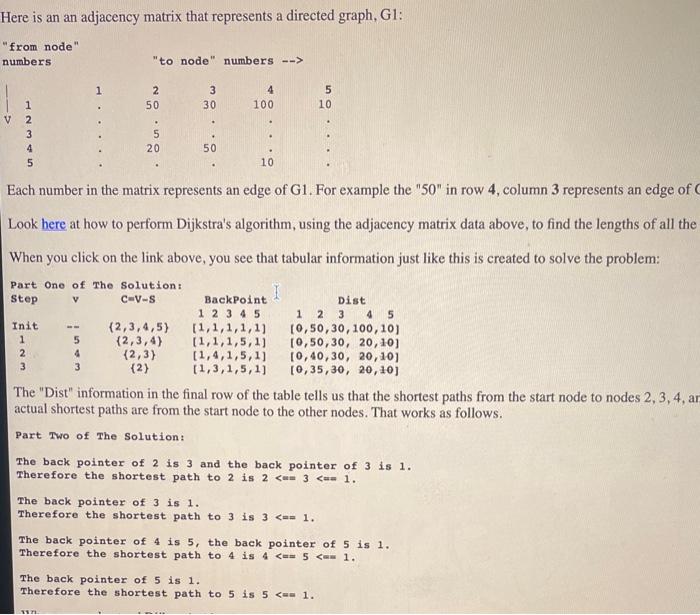
Here is an an adjacency matrix that represents a directed graph, G1: Each number in the matrix represents an edge of G1. For example the "50" in row 4, column 3 represents an edge of Look bere at how to perform Dijkstra's algorithm, using the adjacency matrix data above, to find the lengths of all the When you click on the link above, you see that tabular information just like this is created to solve the problem: The "Dist" information in the final row of the table tells us that the shortest paths from the start node to nodes 2,3,4, a actual shortest paths are from the start node to the other nodes. That works as follows. Part Two of The Solution: The back pointer of 2 is 3 and the back pointer of 3 is 1 . Therefore the shortest path to 2 is 2