Question
Using the Matlab code provided please fill out the table for equations a,b,c and d. Thank you in advance! function [root, ea, iter] = newtraph(func,
Using the Matlab code provided please fill out the table for equations a,b,c and d. Thank you in advance!

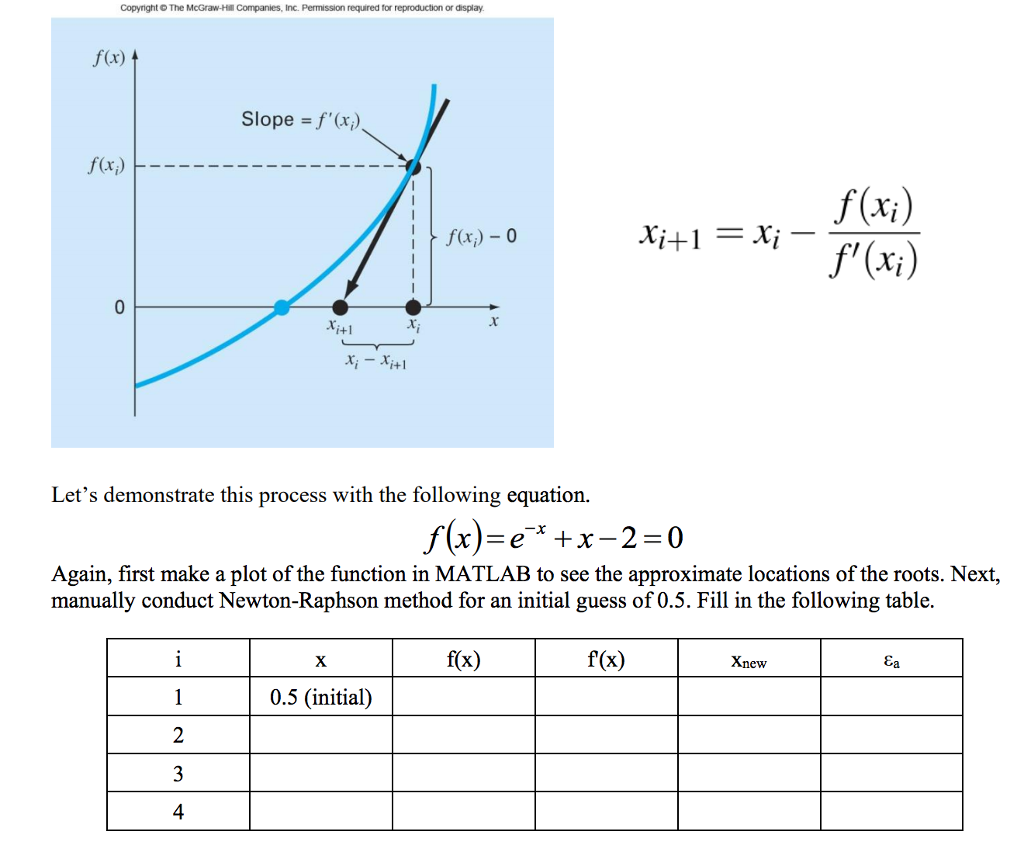
function [root, ea, iter] = newtraph(func, dfunc, xr, es, maxit) % newtraph: Newton-Raphson root finding method % [root, ea, iter] = newtraph(func, dfunc, xr, es, maxit) % input: % func = name of function % dfunc = name of derivative of function % xr = initial guess % es = desired relative error (default = 0.0001%) % maxit = maximum allowable iterations (default = 20) % output: % root = real root % ea = approximate relative error (%) % iter = number of iterations % a text file 'newtraph_out.txt' is generated to store iterations if nargin Type in the following code, fill in the blank, and create a function m-file named newtraph.m function [root, ea, iter] = newt raph (func, drunc, xr, es, maxit) % newt rap: Newton-Raphson root finding method % [root, ea, iter] = newtraph (func, drunc, xr, es, maxit) % input: % func = name of function % dfunc name of derivative of function 8 xrinitial guess % es - desired relative error (default 0.0001%) % maxit = maximum allowable iterations (default 20) output: root = real root % ea approximate relative error (%) % iter number of iterations % a text file 'newtraph-out.txt' is generated to store iterations if nargin>f-e (x) exp (-x) +x-2; >> df- e (x) -exp (x) +1; >>fplot(f, [-2 10]); grid on; >>root, ea, iter] newtraph (f, df, 0.5) 3. Solve the following problems with Newton-Raphson method function (a) cos(x)-x-0 (b) x*-x-2-0 (find both roots by trying different initial guesses) (c) x*-2x +1-0 (notice this is a double root, and it takes unusually large number of iterations.) (d) 2x -2-0 (notice this is a derivative of equation (c), giving the same root but much faster.) Type in the following code, fill in the blank, and create a function m-file named newtraph.m function [root, ea, iter] = newt raph (func, drunc, xr, es, maxit) % newt rap: Newton-Raphson root finding method % [root, ea, iter] = newtraph (func, drunc, xr, es, maxit) % input: % func = name of function % dfunc name of derivative of function 8 xrinitial guess % es - desired relative error (default 0.0001%) % maxit = maximum allowable iterations (default 20) output: root = real root % ea approximate relative error (%) % iter number of iterations % a text file 'newtraph-out.txt' is generated to store iterations if nargin>f-e (x) exp (-x) +x-2; >> df- e (x) -exp (x) +1; >>fplot(f, [-2 10]); grid on; >>root, ea, iter] newtraph (f, df, 0.5) 3. Solve the following problems with Newton-Raphson method function (a) cos(x)-x-0 (b) x*-x-2-0 (find both roots by trying different initial guesses) (c) x*-2x +1-0 (notice this is a double root, and it takes unusually large number of iterations.) (d) 2x -2-0 (notice this is a derivative of equation (c), giving the same root but much faster.)
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


