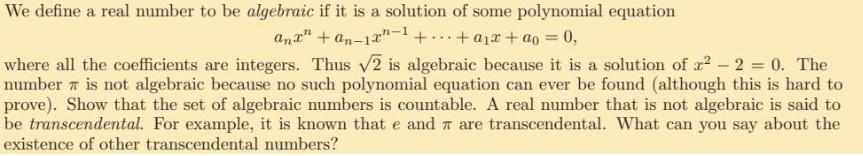
We define a real number to be algebraic if it is a solution of some polynomial equation Anx" + an1x+...+ x + ao = 0, where all the coefficients are integers. Thus 2 is algebraic because it is a solution of r - 2 = 0. The number is not algebraic because no such polynomial equation can ever be found (although this is hard to prove). Show that the set of algebraic numbers is countable. A real number that is not algebraic is said to be transcendental. For example, it is known that e and are transcendental. What can you say about the existence of other transcendental numbers?