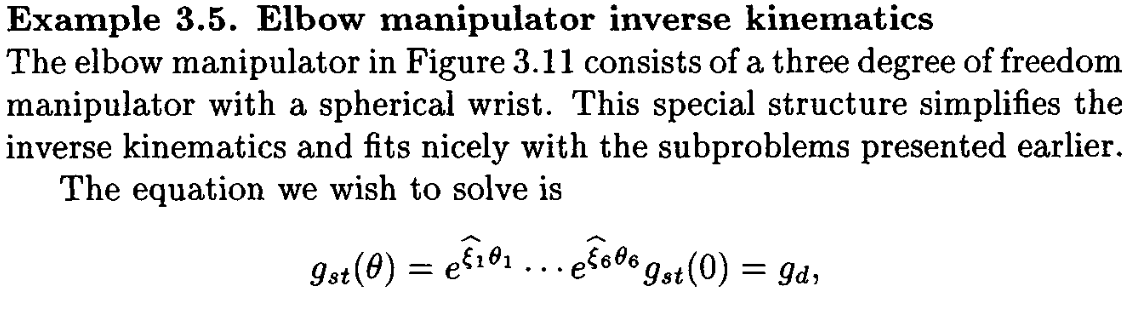
We will consider Example 3.5 in MLS (inverse kinematics of the elbow manipulator). Assume lo = 1 = = 1. And the desired pose of the end-effector is 9d )). 0.5 1.2 1.1 R(0.2 rad) R (0.4 rad) OT Find all the inverse kinematics solutions. You will need to write a Matlab script with Matlab functions for each subproblem. Example 3.5. Elbow manipulator inverse kinematics The elbow manipulator in Figure 3.11 consists of a three degree of freedom manipulator with a spherical wrist. This special structure simplifies the inverse kinematics and fits nicely with the subproblems presented earlier. The equation we wish to solve is 9st (0) = gst(0) = Id, e Captured with Xnip $ S lo E 1 --- $4 3 12 196 Figure 3.11: Elbow manipulator. Apol qw - where ga SE(3) is the desired configuration of the tool frame. Post- multiplying this equation by 9 (0) isolates the exponential maps: ef0... es gagst (0) =: 91. We determine the requisite joint angles in four steps. Step 1 (solve for the elbow angle, 03). Apply both sides of equation (3.30) to a point pw E R which is the common point of intersection for the wrist axes. Since exp(0)pw = pw if pw is on the axis of , this yields 10 202 303 pw = 91Pw. (3.31) Subtract from both sides of equation (3.31) a point p, which is at the intersection of the first two axes, as shown in Figure 3.11: e0030w Pb = e0 202 (e03pw - Pb) 202 ( || e$ 303, Pw $5 to $6 Pw - Pb|| = ||91Pw Pb||. - (3.30) Using the property that the distance between points is preserved by rigid motions, take the magnitude of both sides of equation (3.32): = 91Pw - Pb. (3.32) (3.33) This equation is in the form required for Subproblem 3, with p = Pw, q = Pb, and 6 = ||91Pw - Pb||. Applying Subproblem 3, we solve for 03. Step 2 (solve for the base joint angles). Since 03 is known, equation (3.31) becomes ef101 202 (ef303 pw) = 91.pw. (3.34) exp(303)pw and q = 9Pw gives the Step 3 (solve for two of three wrist angles). The remaining kinematics can be written as Applying Subproblem 2 with p = values for and 02. -1 04 05 06 = e-303 e-202e-101 gag=+ (0) =: 92. (3.35) Apply both sides of equation (3.35) to a point p which is on the axis of 6 but not on the 4, 5 axes. This gives 404 505 p = 92P. Apply Subproblem 2 to find 04 and 05. Step 4 (solve for the remaining wrist angle). The only remaining un- known is 06. Rearranging the kinematics equation and applying both sides to any point p which is not on the axis of $6, ga9st (0)p =: q. escoop 2-E505 e - 04... e- e-101 (3.36) 'p = e' (3.37) Apply Subproblem 1 to find 06. At the end of this procedure, 0 through 06 are determined. There are a maximum of eight possible solutions, due to multiple solutions for equations (3.33), (3.34), and (3.36). Note that the overall procedure is to first solve for the three angles which determine the position of the center of the wrist and then solve for the wrist angles.