Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Solve and show work:) 19. f'(x) = lim f(x+h)-f(x) h 3h lim ho h =lim 3=3 A-0 H lim A-0 Domain off domain of f'
Solve and show work:)
![[ begin{aligned} f^{prime}(x) &=lim _{h ightarrow 0} frac{f(x+h)-f(x)}{h}=lim _{h ightarrow 0} frac{[3(x+h)-8]-(3](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2022/08/62fe0ec97c5ef_1660817094521.jpg)
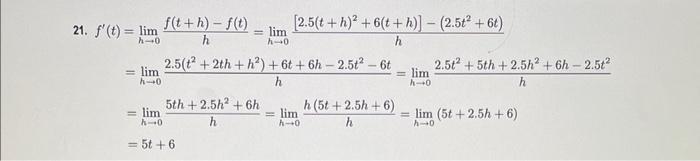
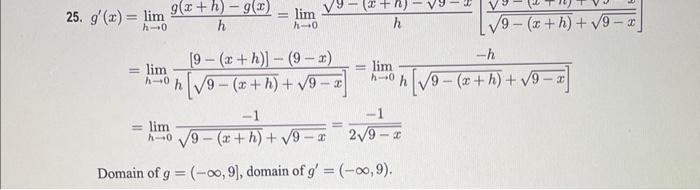
19. f'(x) = lim f(x+h)-f(x) h 3h lim ho h =lim 3=3 A-0 H lim A-0 Domain off domain of f' = R.. [3(x+h)-8]-(3x-8) h 11 lim 3x +3h 8-3x+8 - h
Step by Step Solution
★★★★★
3.32 Rating (152 Votes )
There are 3 Steps involved in it
Step: 1
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Principles of Marketing
Authors: Philip Kotler, Gary Armstrong
14th Edition
132167123, 132997266, 9780132997263, 978-0132167123
