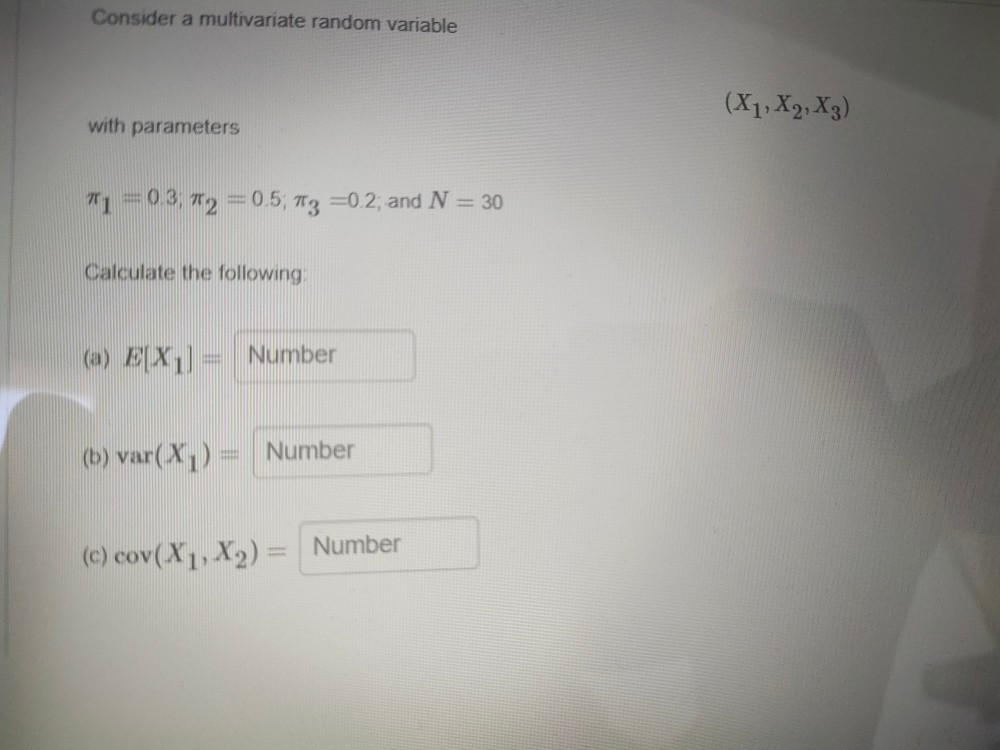
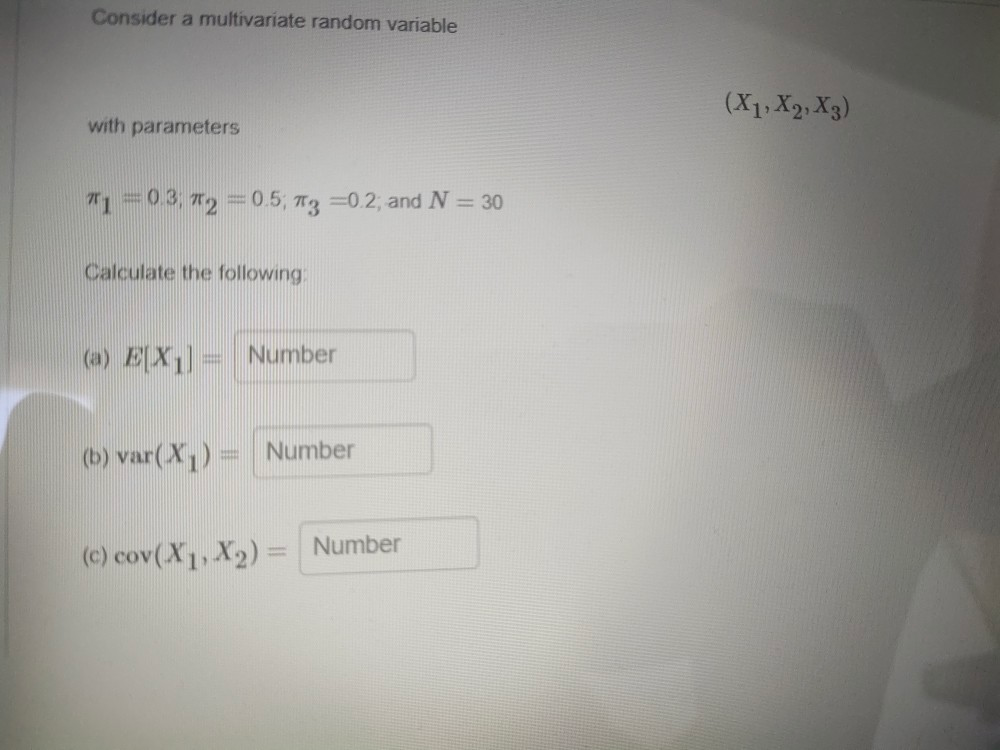
Question
What is meant by the term nominal design in connection with a radial flow gas turbine rotor? Sketch the velocity diagrams for a 90 IFR


What is meant by the term nominal design in connection with a radial flow gas turbine rotor? Sketch
the velocity diagrams for a 90 IFR turbine operating at the nominal design point. At entry to a 90
IFR turbine the gas leaves the nozzle vanes at an absolute flow angle, ?2, of 73. The rotor blade tip
speed is 460 m/s and the relative velocity of the gas at rotor exit is twice the relative velocity at rotor
inlet. The rotor mean exit diameter is 45% of the rotor inlet diameter. Determine,
(i) the exit velocity from the rotor;
(ii) the static temperature difference, T2 - T3, of the flow between nozzle exit and rotor exit.
Assume the turbine operates at the nominal design condition and that Cp 1.33 kJ/kg K.
10. The initial design of an IFR turbine is to be based upon Whitfield's procedure for optimum efficiency. The turbine is to be supplied with 2.2 kg/s of air, a stagnation pressure of 250 kPa, a stagnation temperature of 800C, and have an output power of 450 kW. At turbine exit the static
pressure is 105 kPA. Assuming for air that ? 1.33 and R 287 J/kg K, determine the value
of Whitfield's power ratio, S, and the total-to-static efficiency of the turbine



Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


