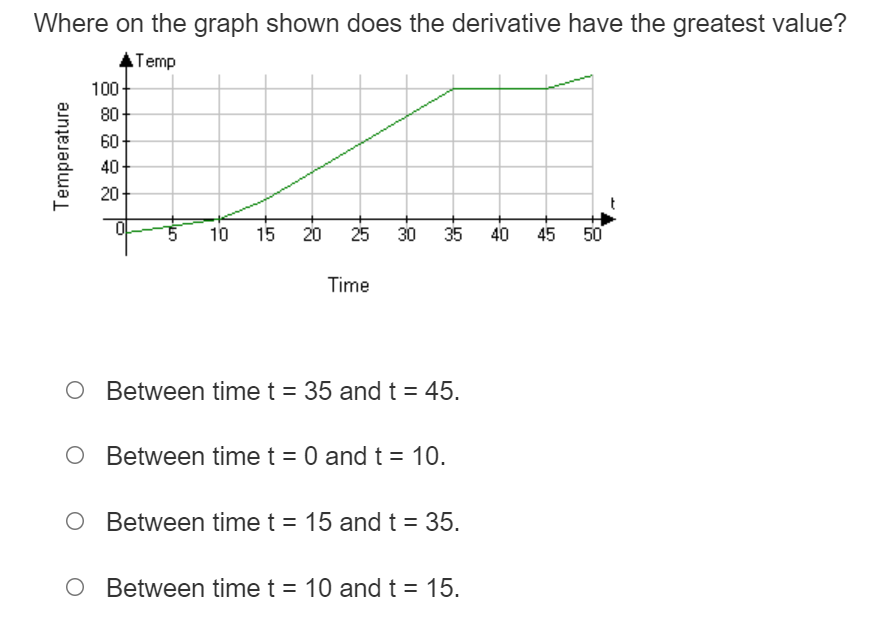
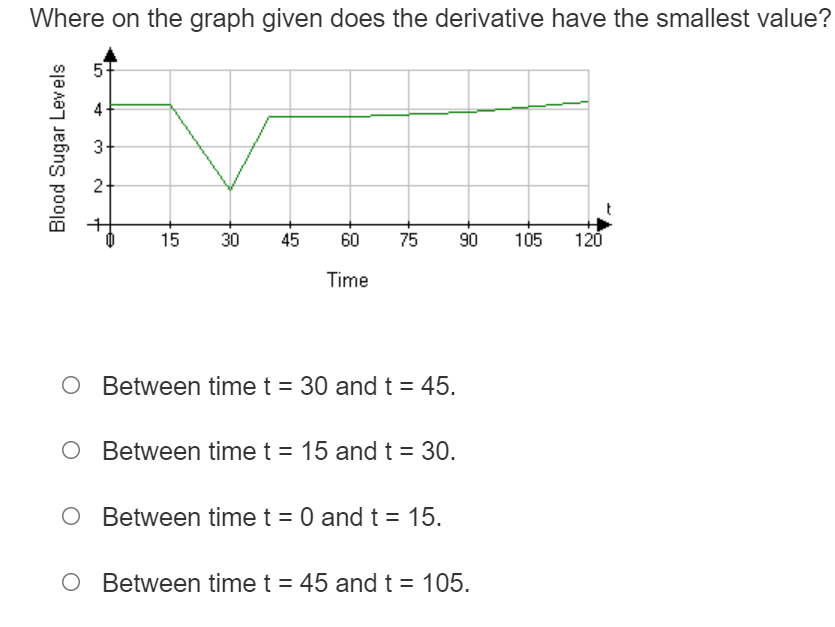
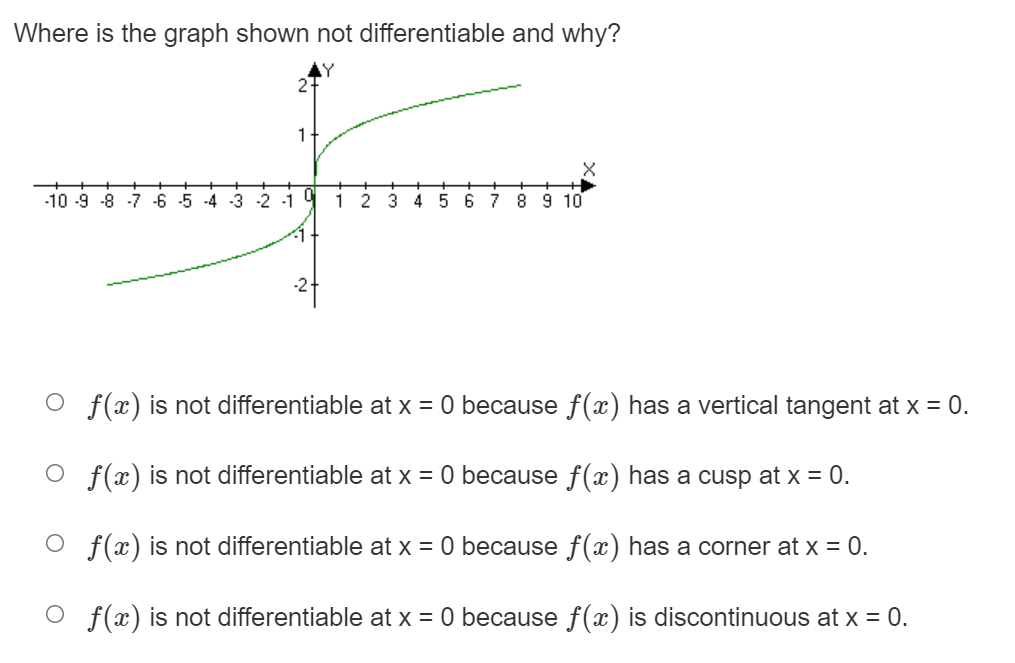
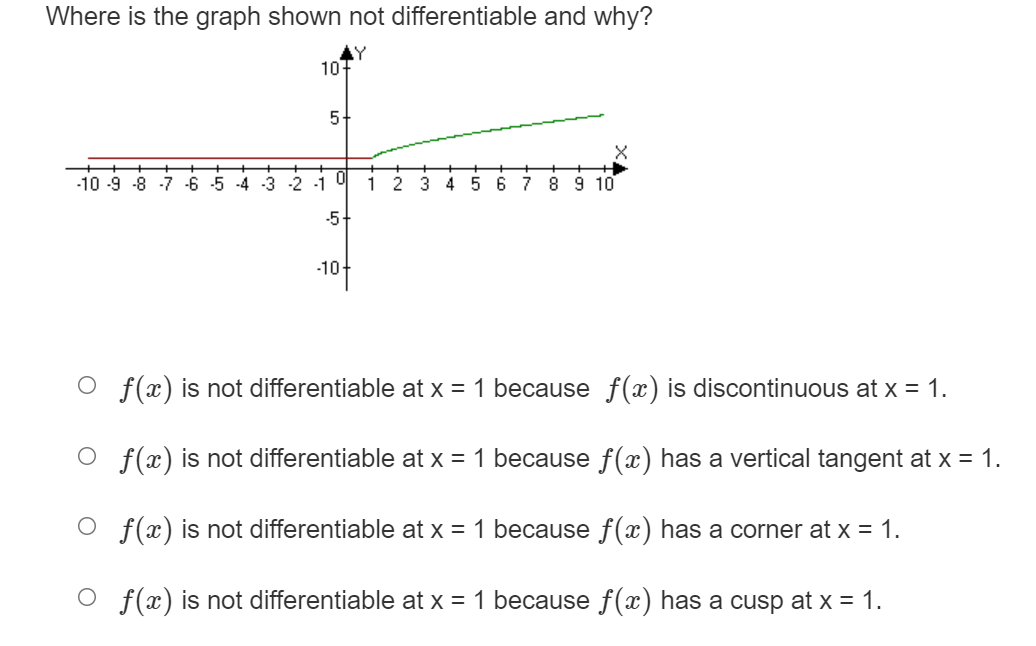
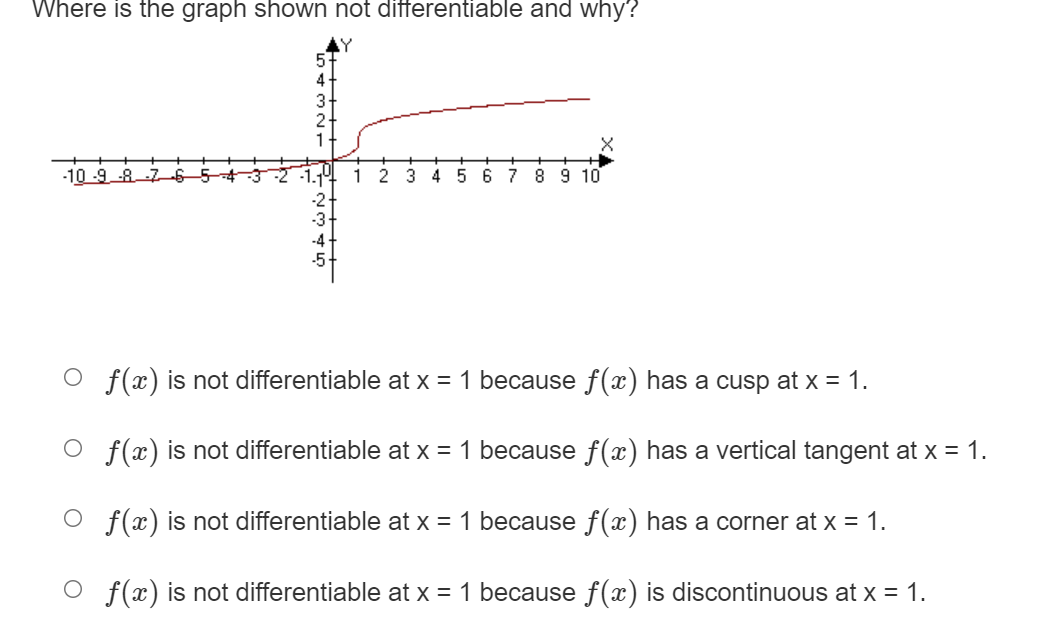
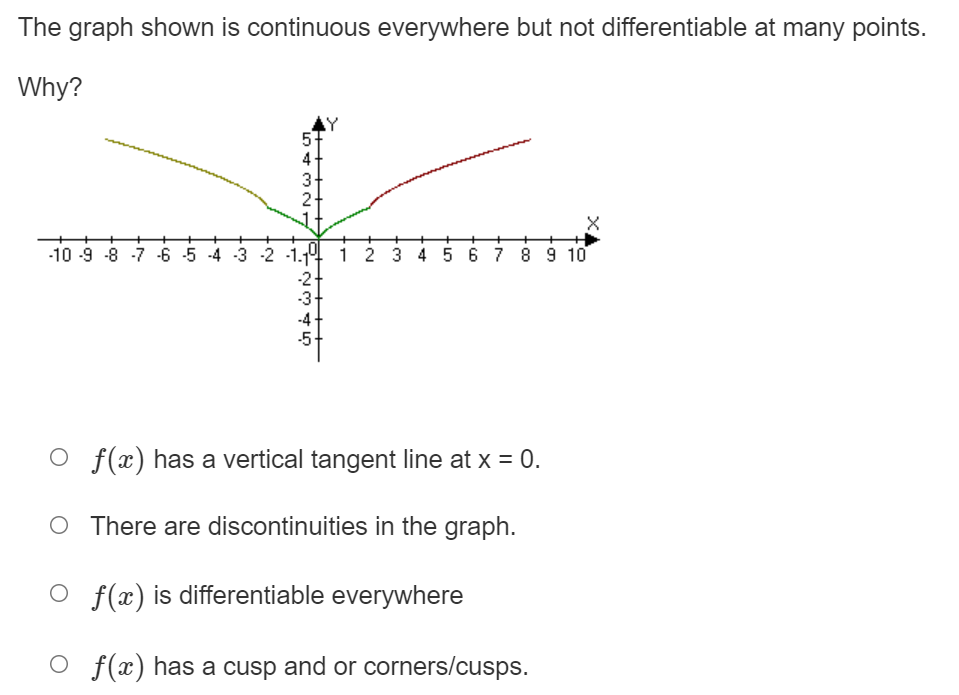
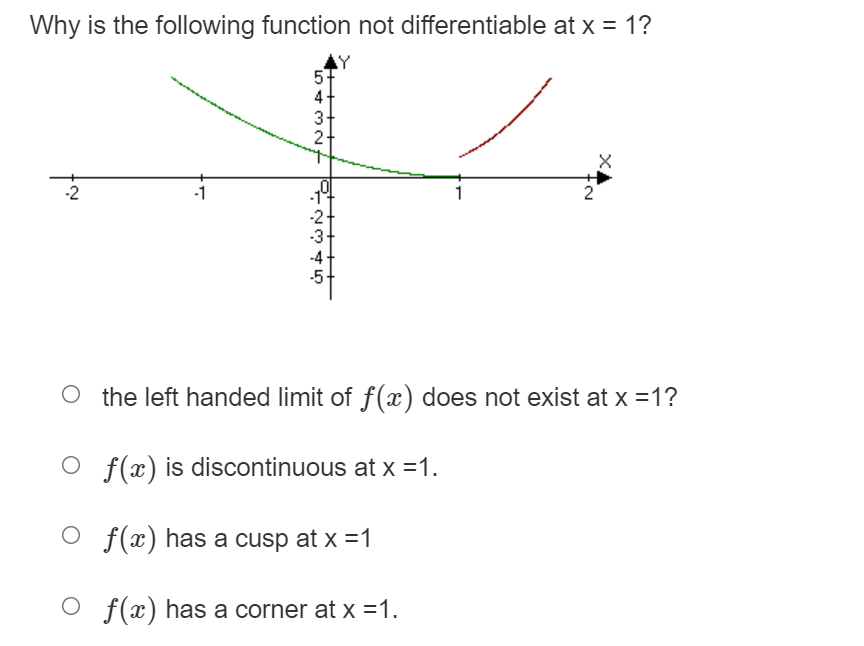
Where on the graph shown does the derivative have the greatest value? Temperature 0 Between time t = 35 and t = 45. 0 Between time t = 0 and t = 10. 0 Between time t = 15 and t = 35. 0 Between time t = 10 and t = 15. Where on the graph given does the derivative have the smallest value? Blood Sugar Levels N 15 30 45 60 75 90 105 120 Time O Between time t = 30 and t = 45. O Between time t = 15 and t = 30. O Between time t = 0 and t = 15. O Between time t = 45 and t = 105.f (ac) = lim h f(ath)-f(3) if f(ac) = Jac|. Use the definition of the derivative to determine if the function is differentiable at x = 0 h-+0 o f(a) is not differentiable at x = 0 because the lim f( xth) -f(I) = 00 at X = 0. h-+0 h o f(a) is not differentiable at x = 0 because the lim f(xth) -f(x) h increases without bound at x = 0. h-c O f(x) is differentiable at x = 0. o f(a) is not differentiable at x = 0 because the lim f( ath)-f(x) h-+c h is not the same from the right and left.Where is the graph shown not differentiable and why? X -10 -9 -8 7 6 5 4 -3 2 -1 9 1 2 3 4 5 6 7 8 9 10 O f(ac) is not differentiable at x = 0 because f(a ) has a vertical tangent at x = 0. O f(ac) is not differentiable at x = 0 because f(a) has a cusp at x = 0. O f (ac) is not differentiable at x = 0 because f(a ) has a corner at x = 0. O f (ac) is not differentiable at x = 0 because f (a ) is discontinuous at x = 0.Which statement below is true? 0 It is possible for a function to be differentiable but not continuous. 0 If a function is differentiable everywhere then it must be continuous. 0 If a graph is continuous then it must be differentiable. O A cusp is a point where the graph is not continuous. Where is the graph shown not differentiable and why? O m) is not differentiable at x = 1 because f(a:) is discontinuous at x = 1. 0 x) is not differentiable at x = 1 because x) has a vertical tangent at x = 1. 0 re) is not differentiable at x = 1 because x) has a corner at x = 1. 0 re) is not differentiable at x = 1 because x) has a cusp at x = 1. Where is the graph shown not differentiable and why? Y it WA UT -10 -9 8 76 3 4 5 6 7 8 9 10 O f (ac) is not differentiable at x = 1 because f(a ) has a cusp at x = 1. O f(ac) is not differentiable at x = 1 because f(a) has a vertical tangent at x = 1. O f (x) is not differentiable at x = 1 because f(a ) has a corner at x = 1. O f(x) is not differentiable at x = 1 because f(a) is discontinuous at x = 1.2, - 10