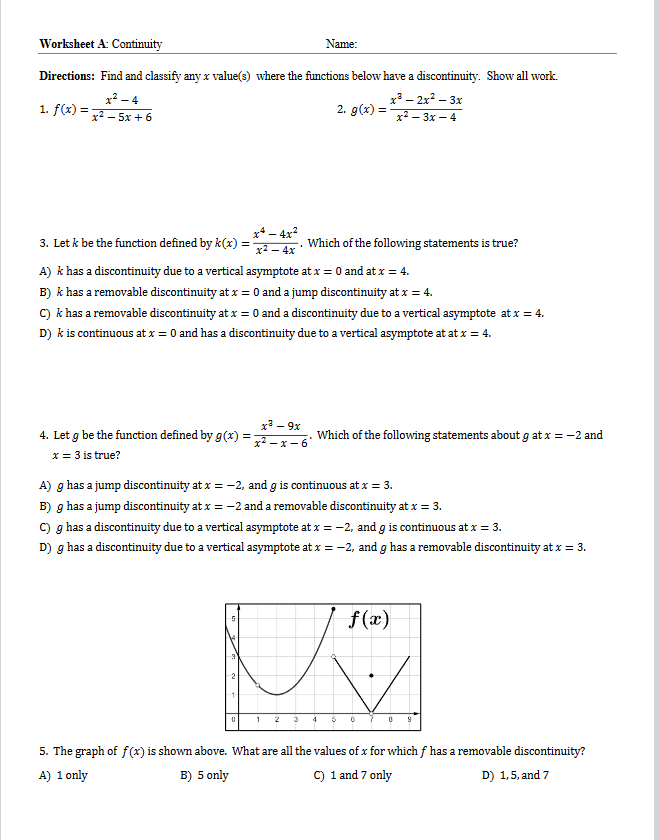
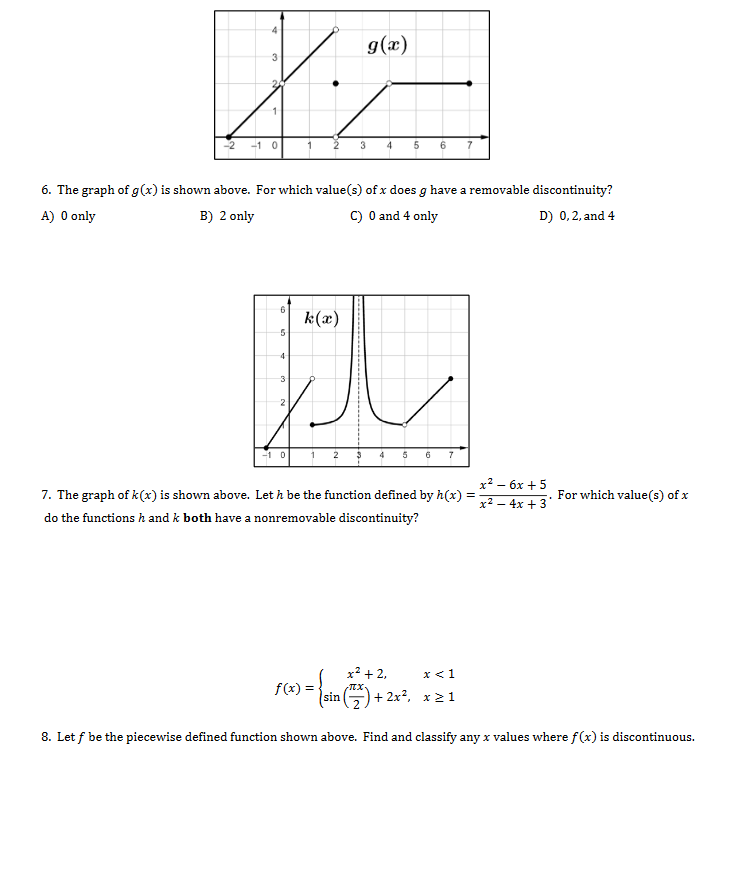
Worksheet A: Continuity Name: Directions: Find and classify any x value(s) where the functions below have a discontinuity. Show all work. ri -4 2. g(x) = x - 2x - 3x 1. f (x) = = x2 - 5x + 6 x2 - 3x - 4 3. Let & be the function defined by k(x) = = x* - 4x2 x2 - 4x . Which of the following statements is true? A) * has a discontinuity due to a vertical asymptote at x = 0 and at x = 4. B) k has a removable discontinuity at x = 0 and a jump discontinuity at x = 4. C) k has a removable discontinuity at x = 0 and a discontinuity due to a vertical asymptote at x = 4. D) & is continuous at x = 0 and has a discontinuity due to a vertical asymptote at at x = 4. x3 - 9x 4. Let g be the function defined by g(x) = ; x2 -x-6' . Which of the following statements about g at x = -2 and x = 3 is true? A) g has a jump discontinuity at x = -2, and g is continuous at x = 3. B) g has a jump discontinuity at x = -2 and a removable discontinuity at x = 3. C) g has a discontinuity due to a vertical asymptote at x = -2, and g is continuous at x = 3. D) g has a discontinuity due to a vertical asymptote at x = -2, and g has a removable discontinuity at x = 3. f (x) 2 2 5. The graph of f(x) is shown above. What are all the values of x for which f has a removable discontinuity? A) 1 only B) 5 only C) 1 and 7 only D) 1,5, and 73 g(x) -1 3 5 6 6. The graph of g(x) is shown above. For which value(s) of x does g have a removable discontinuity? A) 0 only B) 2 only C) 0 and 4 only D) 0, 2, and 4 k(x) -4 3 2 1 0 2 5 4 5 6 7 7. The graph of k(x) is shown above. Let h be the function defined by h(x) = = x2 - 6x + 5 x2 - 4x + 3 . For which value(s) of x do the functions h and & both have a nonremovable discontinuity? * 2 + 2 , x 0 9. Let h be the piecewise defined function shown above. Find and classify any x values where h(x) is discontinuous. x' - 1 k(x) = {x2 - 3x -4' x 3 11. Let f be the piecewise defined function shown above and let c be a positive constant. Find the value of c such that f (x ) has a hole at x = 3.f ( x ) = 17 -3x, x21 12. The piecewise function f (x) is given above. Is f (x) continuous at x = 1? Give a reason for your answer. g (x) = =cos(x) - 3, x 0 x2 - 1, x>0 13. The piecewise function g(x) is given above. Is g(x) continuous at x = 0? Give a reason for your answer. h(x)= juxta, x