"Write an introduction"

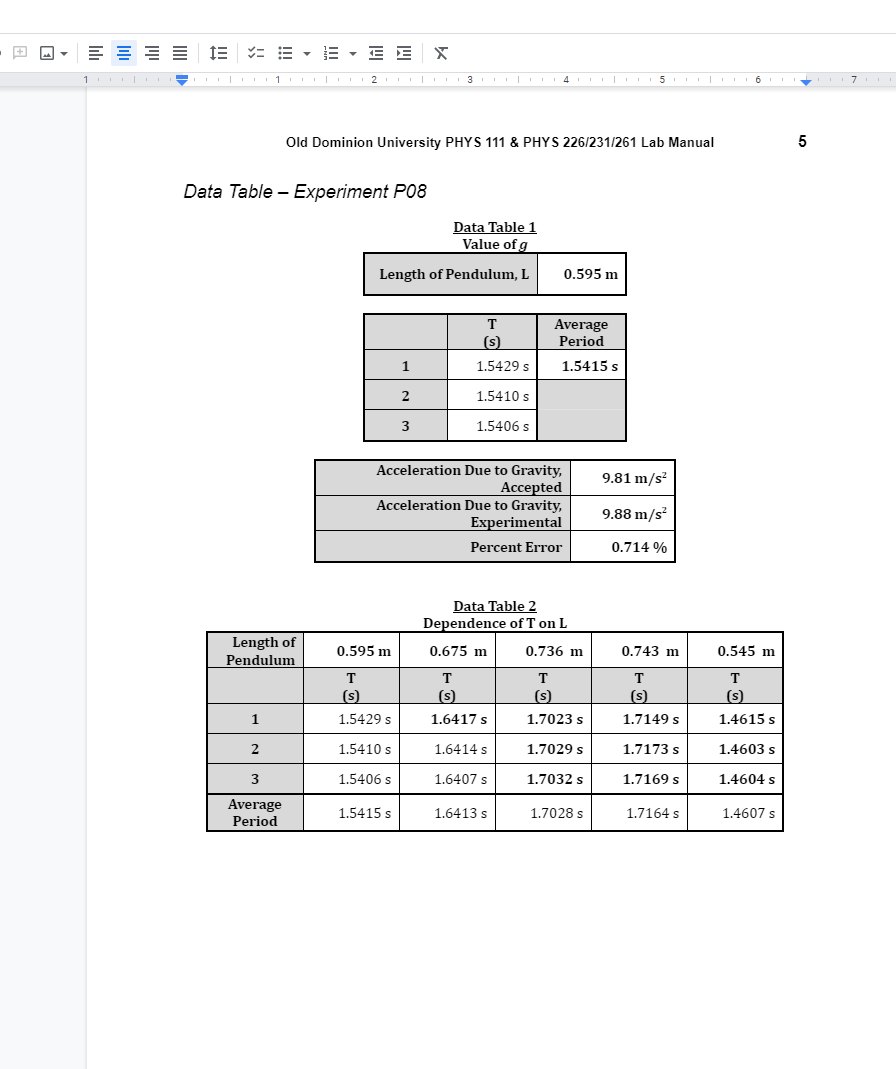
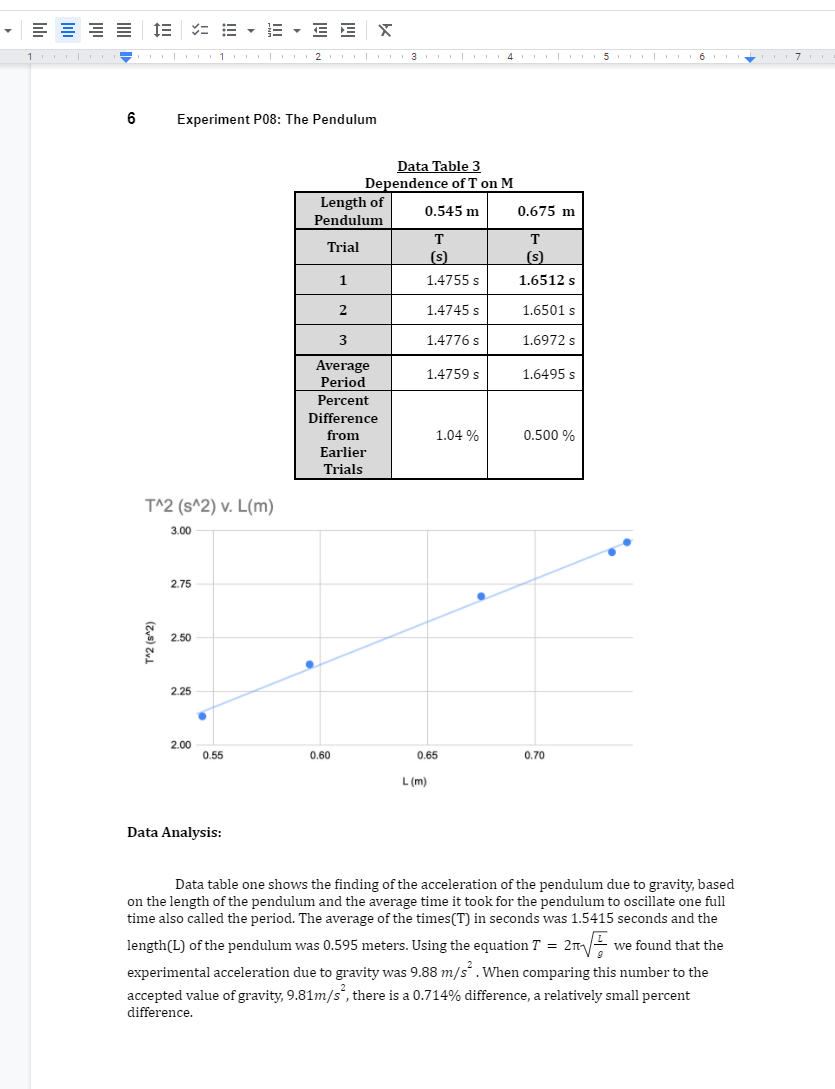
1 7 1 2 Experiment P08: The Pendulum The Pendulum Experiment P08 Objective Investigate the simple harmonic motion of a pendulum and factors that influence its period of oscillation Materials Photogate Timer Pendulum Hanger Photogate Timer Power Supply Universal Table Clamp Lab Support Rod, 36" Meter Stick Pendulum Theory The simple pendulum is a favorite introductory exercise because Galileo's experiments on pendulums in the early 1600s are usually regarded as the beginning of experimental physics. A simple pendulum consists of a mass m hanging at the end of a string of length L. The period of a pendulum or any oscillatory motion is the time required for one complete cycle, that is, the time to go back and forth once. If the amplitude of motion of the swinging pendulum is small, then the pendulum behaves approximately as a simple harmonic oscillator, and the period T of the pendulum is given approximately by T = 2TV/_ (1) where g is the acceleration due to gravity (9.81 m/s ) and Z is the length of the pendulum. This expression holds true for small amplitudes of oscillation. We will also test larger amplitudes to see the effects. It is important that during this experiment you keep the amplitude of the pendulum's swing small. There is a dependence of the pendulum's period on the amplitude of the swing (i.e. - the angle it swings). This is given by the equation below, and 0 is measured in radians. For small angles, the second and third terms within the brackets are minimal and can be ignored. This then gives us equation (1), but, again, only when the amplitude of the pendulum is small. T = 2n.[1 + 7587 + 3072 07] (2) Procedure Part A: The Simple Pendulum Here we will use a timer to take measurements of the period of oscillation of a pendulum. We will investigate pendulums of various lengths and swinging at different amplitudes. 1. Using a table clamp, metal rod, and a pendulum hanger, set up your equipment according to Figure P08.1.Old Dominion University PHYS 111 a PHYS 226E31I251 Lab Manual 3 Set the timer [below the pendulum in the photo) to he on PEND mode. {This stands for 'pendulum'. The timer will start when something passes through. it will ignore the next time the pendulum passes through. and then it will stop counting on the third pass. This will he the time for one. full hackandforth swing.) Data Collection Technique Position the photogate carefully so that the mass at the end of the pendulum passes directly through the diodes of the photogate. After pulling the mass to the side. release it carefully so that it swings through the photogate without a collision. Amv the mass to swing back and forth a few times before making measurements to allow any wobble to settle out. After the mass is swinging several measurements of T can he quickly made by simply pressing the reset button while the mass is still swinging. You should not stop the mass and restart it alter each measurement, since this will introduce unnecessary wobble. Always keep an eye on the pendulum while it is swinging so that it does not drift into a collision with the delicate. and expensive. photogate. Determination ofg 3 . First. we will determine 9 from equation [1}. The pendulum is on a long string attached to the hanger. To lengthenfshorten the string you can wrap it around the hanger to get the length needed. Choose a \"ll\" pendulum length you want and then measure the distance L from P\" the hanger to the middle of the hall on the string Record this in Data Table 1. Set the pendulum swinging with a small amplitude. {Pull back just a few degrees. [ust enough to pass completely through the photogate with each swing.) Make three measurements of the period T. Use your average period. along with equation [1], and determine acceleration of gravity. 9. Calculate the percent error ofyour value with the know value {9.81 mfsz). Dependenoe otl'T on L 6. How determine the dependence of the period on the length of the pendulum. [.engthen and shorten the pendulum as needed. measure L and T for each of the 5 pendulum lengths you chose. Keep the amplitude of motion very small so that equation [1} is approximately correct Using your data, make a graph of '1'2 vs. I... Use your graphing program to determine the slope of your graph. Compare your slope to equation 1 and discuss how your slope can again he used to nd the acceleration due to gravity. 9. Dependence of T on Mass 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 3 1 1 1 1 1 1 14 15 1 1 1|1 1 16 1 1 171 1 17 1 Old Dominion University PHYS 111 & PHYS 226/231/261 Lab Manual 5 Data Table - Experiment P08 Data Table 1 Value of g Length of Pendulum, I 0.595 m T Average (s ) Period 1 1.5429 s 1.5415 s 2 1.5410 s 3 1.5406 s Acceleration Due to Gravity, 9.81 m/s Accepted Acceleration Due to Gravity, Experimental 9.88 m/s- Percent Error 0.714 % Data Table 2 Dependence of T on I Length of 0.595 m 0.675 m 0.736 m 0.743 m 0.545 m Pendulum T T T T T (s ) (S ) (S ) (s ) (s) 1 1.5429 s 1.6417 s 1.7023 s 1.7149 s 1.4615 s 2 1.5410 s 1.6414 s 1.7029 s 1.7173 s 1.4603 s 3 1.5406 1.6407 s 1.7032 s 1.7169 s 1.4604 s Average 1.5415 s 1.6413 s 1.7028 s 1.7164 s 1.4607 s PeriodE 1 121 1 1|1 1 13 1 1 1 1 1 1 1 1 17 6 Experiment P08: The Pendulum Data Table 3 Dependence of T on M Length of Pendulum 0.545 m 0.675 m Trial T T (s ) 1 1.4755 s 1.6512 s 2 1.4745 s 1.6501 s 3 1.4776 s 1.6972 s Average Period 1.4759 s 1.6495 s Percent Difference from 1.04% 0.500 % Earlier Trials T^2 (S^2) v. L(m) 3.00 2.75 2.50 T 2 (5*2) 2.25 2.00 0.55 0.60 0.65 0.70 L (m) Data Analysis: Data table one shows the finding of the acceleration of the pendulum due to gravity, based on the length of the pendulum and the average time it took for the pendulum to oscillate one full time also called the period. The average of the times(T) in seconds was 1.5415 seconds and the length(L) of the pendulum was 0.595 meters. Using the equation T = 2n- we found that the experimental acceleration due to gravity was 9.88 m/s" . When comparing this number to the accepted value of gravity, 9.81m/s, there is a 0.714% difference, a relatively small percent difference.Old Dominion University PHYS 111 & PHYS 226/231/261 Lab Manual Data table two shows the dependence of the period on the length of the pendulum with the same weight each time. The length of the pendulum was changed five times, and each time the length was changed a period was measured three times in order to find the average period for each length. The closer the pendulum length was to another, the closer the average period was. For example, when the length was at 0.736m, the average period was 1.7028s and when the length was 0.743, the average period was 1.7164s, only a 0.0136 second difference. Data table three tested how the period changes when there was a lighter mass at the end of the pendulum. The lengths of the pendulum were the same, 0.545m and 0.675 meters. The average time of each period did not vary much. For the 0.545 length, the percent difference was 1.04% and for the 0.675 length, the percent difference was 0.500%. Although not very large differences, the average times of the lighter mass had higher period times. Conclusion Our goal during the experiment was to observe the simple harmonic motion of a pendulum and factors that influence its period of oscillation. We did this by using the pendulum and photogate to record the measurements of its period of oscillation. In the first data table it was recorded that the Length of Pendulum was at 0.595 m. During the first trial it took 1.5429 s, the second trial took 1.5410 s, and the third trial took 1.5406 s. This averages out at a total of 1.5415 s for all three trials. The percent error between the accepted and experimental acceleration due to gravity was 0.714 percent. For the second table the length of we observed the dependence of the period on the length of the pendulum. This was recorded at various lengths. The first length was 0.595 m; the first trial was 1.5429 s, the second trial was 1.5410 s, and the third trial was at 1.5406 s. The average of all three of the trials was 1.5415 s. The second length was 0675 m; the first trial was at 1.6417 s, the second trial was at 1.6414 s, and the third trial was at 1.6407 s. The average of all three of the trials was 1.6413 s. The third length was at 0.736 m; the first trial was 1.7023 s, the second trial was 1.7029 s, and the third trial was at 1.7032 s. The average of the three trials was 1.7028 s. The fourth length was at 0.743 m; the first trial was 1.7149 s, the second trial was at 1.7173 s, and the third trial was at 1.7169 s. The three trials averaged out to 1.7164 s. The fifth and final length was at 0.545 m; the first trial was 1.4615 s, the second trial was 1.4603 s, the third trial was 1.4604 s. This averaged out to 1.4607 s. For the second table we looked at the dependence of time on mass. This was recorded at two different lengths. The first one being 0.545 m. For the first trial 1.4755 s was recorded, for the second trial it was 1.4745 s, for the third trial it was 1.4759s. The three trials averaged at 1.4759 s. A percent difference from earlier trials came out to 1.04%. The second and final length was 0.675 m;8 Experiment P08: The Pendulum the first trial was 1.6512 s, the second trial was 1.7501 s, the third trial was 1.6972 s. This averaged out to 1.6495 s. A percent difference from earlier trials came out to 0.500%. These percentages were very low and showed that the data we collected was accurate for what we were working with. This percentage of error is most likely due to friction and air resistance. What to Turn In PHYS 111 and PHYS 226/231/261 Full lab report . Data Tables 1 through 4 Graph of T- vs L Questions to Consider When we measure the period of oscillation, why is it important to keep the amplitude of the swinging pendulum small? How well do your results substantiate the theory that the period of the pendulum is independent of the mass of the ball? Explain. Discuss the energy transformations that occur during one complete oscillation of a simple pendulum. What effect does doubling the length of the string have on the period of a pendulum? Is there a linear correlation or any correlation at all