Write the required functions and script that solve, for a Non-Deterministic Finite Automaton, the same problem that was solved for a Deterministic Finite Automaton in Problem #3 (above). Read about the differences between these two automata (below). Hint: Adapt your code for the FA problem to solve the more general NDFA problem.

A non-deterministic finite automaton (NDFA) is machine described by its states and its transitions: each transition for a statespecifies an input and a set of states (more than one is allowed) that input can lead to: sets with more than one states is what makes it non-deterministic. We can illustrate a NDFA as a graph with state labels in circles and edge labels for transitions (see below). The critical difference between an FA and an NDFA is that an NDFA can have multiple edges with the same label going to different states (we'll see how to represent and simulate such transitions below).

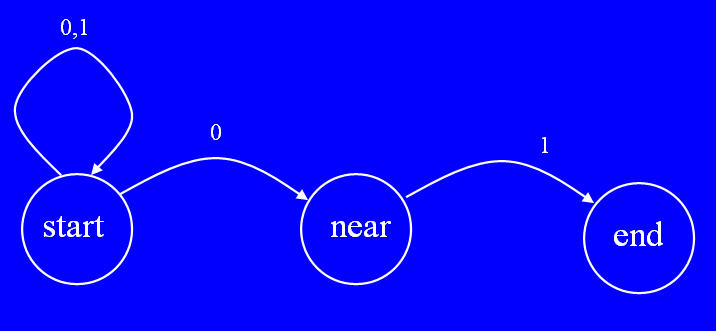
Input and Output:

Read a file that describes a NDFA: each line contains a state and an arbitrary number of input->state transitions. Build a dictionary such that each key is a str state and whose associated value is another dictionary specifying all the transitions from that state: this second dictionary has keys that are str inputs and associated values that are sets of str states: all the states a particular input can lead to. The first token on each line is the str state and the remaining tokens (always coming in pairs) are strinputs and states. All tokens (which can comprise any number of characters) are separated by one semicolon character. We annotate this dictionary as {str:{str:{str}}}.

For example, the input file ndfaendin01.txt contains the following lines (which could appear in this order, or any other and still specify the same NDFA):

 start;0;start;1;start;0;near near;1;end end

Here is a picture of the endin01 NDFA. It graphically illustrates the three states (start, near, and end) and their transitions, using inputs (0 and 1).

Here, the state start is a key in the main dictionary. It's value is a dictionary with two key/value pairs: 0 mapping to the setcontaining start and near, and 1 mapping to the set containing just start. It means that in the start state, if the input is a 0 the NDFA can stay in the start state or it can go to the near state; if the input is a 1 the NDFA must stay in the start state. And similarly the next line means that in the near state, if the input is a 1 the NDFA must go into the end state. The last line means that the end state has no transitions out of it.

Print the NDFA, one state (and its transitions) per line; the states are printed alphabetically and the transition dictionary for each state is printed as a list of input/set of state items (2-tuples) such that these are printed alphabetically by the inputs, and the set of states for each input is printed as an alphabetically sorted list (e.g., near comes before start). Note that the state end is a key in the main dictionary, whose associated transitions are an empty dictionary.

For example, the file above would produce:

 The Contents of the file picked for this Non-Deterministic Finite Automaton end transitions: [] near transitions: [('1', ['end'])] start transitions: [('0', ['near', 'start']), ('1', ['start'])]

Note that there are multiple data files for this program: ndfaendin01.txt and ndfatrain.txt and ndfare.txt;; test/debug your program on the first file; when you are done, test it on the last file. Draw the FA represented by each for to ensure that your code correctly prints and computes with it.

Next, repeatedly read and process lines from a second input file, computing the results of the non-determinisitc finite automaton on the specified start-state with its inputs ; then print out the results in a special form. Each line in the file contains a start-state followed by a sequence of inputs (all separated by semicolons). The start-state will be a state in the FA (it is a key in the outer dictionary) the inputs may specify legal or illegal transitions (may or may not be keys in some inner dictionary).

For example, the input file ndfainputendin01.txt contains the following two lines:

 start;1;0;1;1;0;1 start;1;0;1;1;0;0

For example, the first line means, the start-state is start and the inputs 1, 0, 1, 1, 0, and 1.

The result of processing each line is to print the start-state, and then each input and the new states (plural) it could transition to (the could is what makes it non-deterministic), and finally print the stop-states. For the ndfaendin01 NDFA and the first line in this file, it should print

 Start state = start Input = 1; new possible states = ['start'] Input = 0; new possible states = ['near', 'start'] Input = 1; new possible states = ['end', 'start'] Input = 1; new possible states = ['start'] Input = 0; new possible states = ['near', 'start'] Input = 1; new possible states = ['end', 'start'] Stop state(s) = ['end', 'start']

Note that the set of states it might be in are printed as an alphabetized list. Also note especially that in the start state, if the input is a 0, then the NDFA can either remain in the start state or go into the near state. For this program, we keep track of all states that the NDFA can be in, using a set of new possible states. For the next input, 1, we can be either in the start state (from the start state; an input of 1 allows us to stay in the start state) or the end state (from the near state; an input of 1 allows us to transition to the end state). Thus, we keep track of the set of states the NDFA can be in, and the new set of states the NDFA can be in after processing the next input. In this example, because 'end' is included in the stop-states, this input does end in 01.

For any state that does not have a transition specifying the current input, ignore that input for that state. For example, if near is one of the possible states and 0 is the input, ignore the 0 for the near state.

Functions and Script:

Write the following functions and script. I am providing line counts for these function bodies not as requirements, but to indicate the lengths of well-written Pythonic code.

• read_ndfa has an open (file) parameter; it returns the dictionary representing the non-deterministic finite automaton; hint: I used splicing and the zip function to build the inner dinctionaries, and I called the setdefault function for the inner dict: alternatively I could have built it as defaultdicts from the standard collections module (body is 9 lines).

• ndfa_as_str has a dictionary parameter (representing the FA); it returns a multi-line string (each line is ended by ' '), which when printed shows the contents of the NDFA in the appropriate textual form: sorted alphabetically by state, with a state's transitions sorted by their input values, and sorted by states if an input results in multiple states (body is 4 lines; can you do it in 1?).

• process has a dictionary parameter (representing the NDFA), a str parameter (representing the start-state), and a listparameter (representing a list of str inputs); it returns a list that contains the start-state followed by tuples that show the input and resulting set of states after each transition. For the example shown above, process returns the following list.

   ['start', ('1', {'start'}), ('0', {'near', 'start'}), ('1', {'end', 'start'}), ('1', {'start'}), ('0', {'near', 'start'}), ('1', {'end', 'start'})]

  Finally, remember that if an input is illegal for the current state (is not the key in some transition for the current state), just ignore it. But if the input leads to no possible states (the empty set of states) terminate processing there (body is 12 lines).

• interpret has a list parameter (the list result produced by process); it returns a multi-line string (each line is ended by ' '), which when printed illustrates the results of processing an NDFA on an input in the appropriate textual form. Note that in this output the sets computed in process appear as lists sorted alphabetically by state. See how it prints the example list argument shown above in the Sample Interaction below (body is 5 lines).

• Write a script at the bottom of this module (in if __name__ == '__main__':) that prompts the user to enter the file describing the NDFA, prints it, prompts the user to enter the file containing lines of start-states and input, and simulates the NDFA on each line, printing the results in the appropriate textual form (body is 7 lines).

Sample Interaction:

The program, as specified, will have the following interaction: user-typed information appears in italics. Your output should "match" this one.

 Pick the file name containing this Non-Deterministic Finite Automaton: ndfaendin01.txt The Contents of the file picked for this Non-Deterministic Finite Automaton end transitions: [] near transitions: [('1', ['end'])] start transitions: [('0', ['near', 'start']), ('1', ['start'])] Pick the file name containing a sequence of start-states and subsequent inputs: ndfainputendin01.txt Commence tracing this NDFA from its start-state Start state = start Input = 1; new possible states = ['start'] Input = 0; new possible states = ['near', 'start'] Input = 1; new possible states = ['end', 'start'] Input = 1; new possible states = ['start'] Input = 0; new possible states = ['near', 'start'] Input = 1; new possible states = ['end', 'start'] Stop state(s) = ['end', 'start'] Commence tracing this NDFA from its start-state Start state = start Input = 1; new possible states = ['start'] Input = 0; new possible states = ['near', 'start'] Input = 1; new possible states = ['end', 'start'] Input = 1; new possible states = ['start'] Input = 0; new possible states = ['near', 'start'] Input = 0; new possible states = ['near', 'start'] Stop state(s) = ['near', 'start']

In Week #2 of this course we will cover EBNF and regular expressions, which relate to the files below. You can run these files on your code to ensure they produce the correct results.

The ndfatrain.txt file is a non-deterministic finite automaton that determines whether or not a train (a sequence of characters representing different kinds of cars) is a legal train according to Chapter Exercise #7 in the ENBF lecture. Its input file is ndfainputtrain.txt, which starts with a legal train (one that ends with the state done as one possible state) followed by an illegal train (one that does not end with the state done as one possible state).

The ndfare.txt file is a non-deterministic finite automaton translation of the regular expression ((a*|b)cd)+. Its input file is ndfainputre.txt, which starts with a match (one that ends with the state last as one possible state) followed by a non-match (one that does not end with the state last as one possible state).

0,1 start near end 0,1 start near end