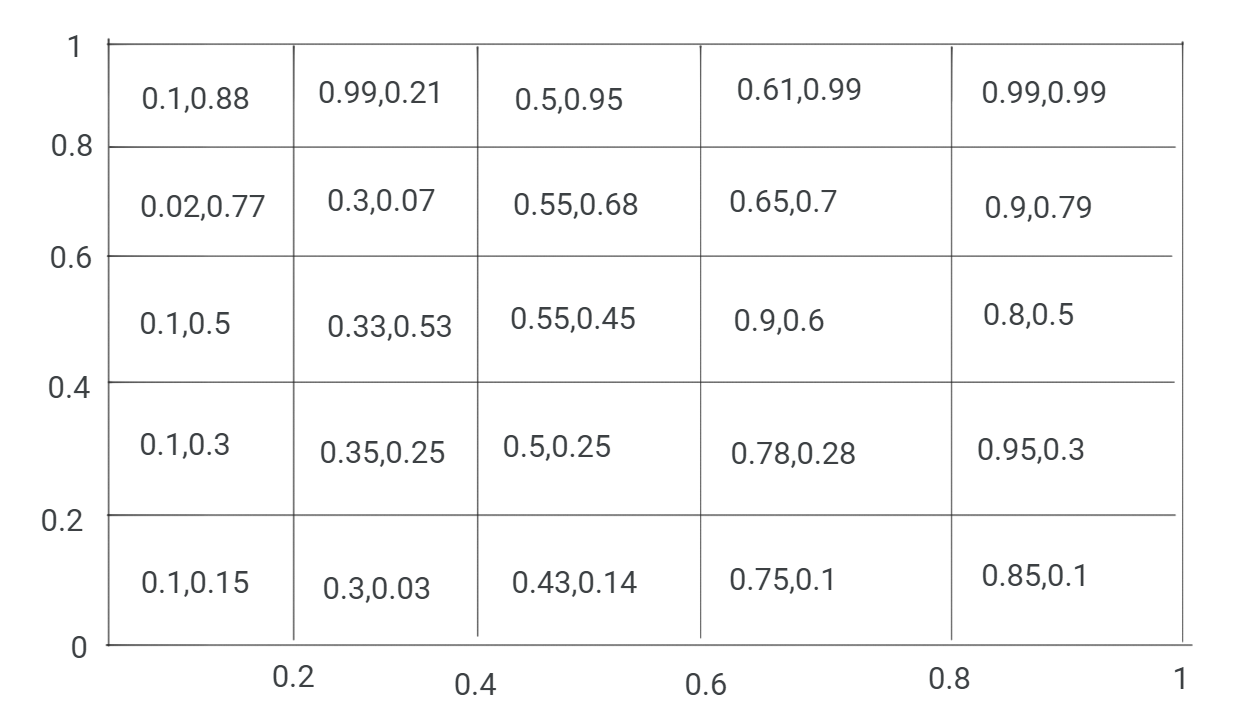
You are eating noodle soup, trying somewhat unsuccessfully to find and extract noodles out of the soup using chopsticks. The noodles have random lengths between 0 and 1 and there are only two noodles left. Find the probability of finding the longer one first. Assume that the probability of obtaining a given noodle equals the length of the noodle divided by the sum of the lengths of all (both, in this case) noodles in the bowl. A. Create a five-by five grid ( 25 cells) that partitions the pairs of a unit square, where is the length of one noodle and y is the length of the other. Determine the probability of obtaining the longer noodle in each of the 25 scenarios. Use these values (with midpoint rule) to estimate the probability in question. B. Set up and evaluate a double integral that will find the exact probability. C. What is the average length of the shorter noodle? D. What is the average length of the longer noodle? E. What is the average of the ratio of the lengths of the short noodle to the long noodle? (This is different from the ratio of the average of their lengths!) F. What is the average of the ratio of the lengths of the long noodle to the short noodle? G. For bonus, you can write a program to answer parts B through F, using an n by n grid, with random lengths in each grid, as we did in class. Use n=100. This will be much more accurate than just selecting 100 random pairs of noodle lengths.(IN JAVA) H. 2nd bonus, repeat part B with 3 noodles, using a triple integral. 1 \begin{tabular}{|l|l|l|l|l|} \hline 0.1,0.88 & 0.99,0.21 & 0.5,0.95 & 0.61,0.99 & 0.99,0.99 \\ \hline 0.02,0.77 & 0.3,0.07 & 0.55,0.68 & 0.65,0.7 & 0.9,0.79 \\ \hline 0.1,0.5 & 0.33,0.53 & 0.55,0.45 & 0.9,0.6 & 0.8,0.5 \\ \hline 0.1,0.3 & 0.35,0.25 & 0.5,0.25 & 0.78,0.28 & 0.95,0.3 \\ \hline 0.1,0.15 & 0.3,0.03 & 0.43,0.14 & 0.75,0.1 & 0.85,0.1 \\ \hline \multicolumn{2}{|c|}{0.2} & \multicolumn{2}{|c|}{0.4} & 0.6 \\ \hline \end{tabular} You are eating noodle soup, trying somewhat unsuccessfully to find and extract noodles out of the soup using chopsticks. The noodles have random lengths between 0 and 1 and there are only two noodles left. Find the probability of finding the longer one first. Assume that the probability of obtaining a given noodle equals the length of the noodle divided by the sum of the lengths of all (both, in this case) noodles in the bowl. A. Create a five-by five grid ( 25 cells) that partitions the pairs of a unit square, where is the length of one noodle and y is the length of the other. Determine the probability of obtaining the longer noodle in each of the 25 scenarios. Use these values (with midpoint rule) to estimate the probability in question. B. Set up and evaluate a double integral that will find the exact probability. C. What is the average length of the shorter noodle? D. What is the average length of the longer noodle? E. What is the average of the ratio of the lengths of the short noodle to the long noodle? (This is different from the ratio of the average of their lengths!) F. What is the average of the ratio of the lengths of the long noodle to the short noodle? G. For bonus, you can write a program to answer parts B through F, using an n by n grid, with random lengths in each grid, as we did in class. Use n=100. This will be much more accurate than just selecting 100 random pairs of noodle lengths.(IN JAVA) H. 2nd bonus, repeat part B with 3 noodles, using a triple integral. 1 \begin{tabular}{|l|l|l|l|l|} \hline 0.1,0.88 & 0.99,0.21 & 0.5,0.95 & 0.61,0.99 & 0.99,0.99 \\ \hline 0.02,0.77 & 0.3,0.07 & 0.55,0.68 & 0.65,0.7 & 0.9,0.79 \\ \hline 0.1,0.5 & 0.33,0.53 & 0.55,0.45 & 0.9,0.6 & 0.8,0.5 \\ \hline 0.1,0.3 & 0.35,0.25 & 0.5,0.25 & 0.78,0.28 & 0.95,0.3 \\ \hline 0.1,0.15 & 0.3,0.03 & 0.43,0.14 & 0.75,0.1 & 0.85,0.1 \\ \hline \multicolumn{2}{|c|}{0.2} & \multicolumn{2}{|c|}{0.4} & 0.6 \\ \hline \end{tabular}