A passive RLC filter is represented by the ordinary differential equation

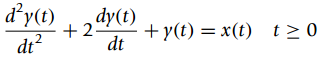
where x(t) is the input and y(t) is the output.

(a) Find the transfer function H(s) of the filter and indicate what type of filter it is.

(b) For an input x(t) = 2u(t), find the corresponding output y(t) and determine the steady-state response.

(c) If the input is x₁(t) = 2[u(t) ˆ’ u(t ˆ’ 1)], express the corre-sponding output y₁(t) in terms of the response y(t) obtained above.

(d) For the above two cases find the difference between the outputs and the inputs of the filter and indicate if this difference signals tend to zero as t increases. If so, what does this mean?

|d²y(t) dy(t) +2- +y(t) = x(t) t > 0 dt dt?