(a) A system is represented by the ordinary differential equation dz(t)/dt = w(t) w(t 1) where w(t) is the input and z(t) the output. i.

(a) A system is represented by the ordinary differential equation dz(t)/dt = w(t) ˆ’ w(t ˆ’ 1) where w(t) is the input and z(t) the output.

i. How is this system related to an averager having an input/output equation

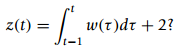
ii. Is the system represented by the given ordinary differential equation LTI?

(b) If we consider the current i(t) the input of a capacitor, with a zero initial voltage across it, the voltage across the capacitor€”or the output€”is given by

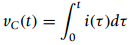
i. Is this capacitor time-invariant? If not, what conditions would you impose to make it time-invariant?

ii. If we let i(t) = u(t) what is the corresponding voltage v_C (t)? If we delay the current source so that the input is i(t ˆ’ 1), find the corresponding voltage across the capacitor and indicate if this result shows the capacitor is time invariant.

(c) An amplitude modulation system has an input/output equation

y(t) = x(t) sin(2Ï€t)            ˆ’ˆž

i. Let x(t) = u(t), plot the corresponding output y(t) = sin(2Ï€t) u(t)

ii. If the input is delayed, i.e., the input is x₁(t) = x(t ˆ’ 0.5) = u(t ˆ’ 0.5), plot the corresponding output y₁(t) = x₁(t) sin(2Ï€t), and use this result to determine whether the given AM system is time-invariant.

z(t) = | w(t)dt + 2? t-1 t-1 vc(t) = : i(t)dt %3D