The following problems relate to linearity, time-invariance, and  causality of systems.

(a) A system is represented by the equation z(t) = v(t) f(t) + B where v(t) is the input, z(t) the output, f(t) a function, and B a constant.

i. Let f(t) = A, a constant. Is the system linear if B ‰  0? linear if B = 0? Explain.

ii. Let f(t) = cos(Ω₀t) and B = 0 is this system linear? time-invariant?

iii. Let f(t) = u(t) ˆ’ u(t ˆ’ 1), the input v(t) = u(t) ˆ’ u(t ˆ’ 1), B = 0, find the corresponding output z(t). Let then the input be delayed by 2, i.e., the input is u(t ˆ’ 2) ˆ’ u(t ˆ’ 3) and f(t) and B be the same, determine the corresponding output. Using these results, is the system time-invariant?

(b) An averager is defined as

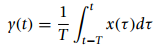
where T > 0 is the averaging interval, x(t) and y(t) are the system input and output.

i. Determine if the averager is a linear system.

ii. Let T = 1, x(t) = u(t), calculate and plot the corresponding output, delay then the input to get x(t ˆ’ 2) = u(t ˆ’ 2), and calculate and plot the corresponding output. From this example, does the system seem time-invariant?€™ Explain. Can you show it in general?

iii. Is this system causal? Give an example to verify your assertion.

Transcribed Image Text:

- x(t)dr y(t) = t-T