A continuous-time LTI system is represented by the ordinary differential equation where x(t) is the input and
Question:
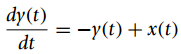
where x(t) is the input and y(t) the output.
(a) Determine the frequency response H(jΩ) of this system by considering the steady-state output of the system to inputs of the form x(t)=ejΩt, for ˆ’ˆž < Ω < ˆž.
(b) Carefully sketch the magnitude, |H(jΩ)|, and the phase, ˆ H(jΩ), frequency responses of the system. Indicate the magnitude and phase at frequencies of 0, ±1, and ±ˆž rad/sec.
(c) If the input to this LTI is x(t) = sin(t)/(Ï€t), determine and carefully plot the magnitude response |Y(Ω)|of the output, indicating the values at frequencies 0, ±1, and ±ˆž rad/sec.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





