Consider the following cases where we want to determine different types of responses.

(a) The input to a LTI system is x(t) = u(t) ˆ’ 2u(t ˆ’ 1) + u(t ˆ’ 2) and the Laplace transform of the output is given by

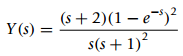
determine the impulse response of the system.

(b) Without computing the inverse of the Laplace transform

corresponding to a causal signal x(t), determine lim_t†’ˆž x(t).

(c) The Laplace transform of the output of a LTI system is

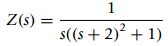
what would be the steady-state response z_ss(t)?

(d) The Laplace transform of the output of a LTI system is

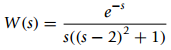
how would you determine if there is a steady state or not? Explain.

(e) The Laplace transform of the output of a LTI system is

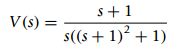
Determine the steady-state and the transient responses corresponding to V(s).

Transcribed Image Text:

(s+ 2)(1 – e=*)? s(s + 1) Y (s) = |X(s) = s(s + 2s + 10)