Control systems attempt to follow the reference signal at the input, but in many cases they cannot follow particular types of inputs. Let the system we are trying to control have a transfer function G(s), and the feedback transfer function be H(s). If X(s) is the Laplace transform of the reference input signal, Y(s) the Laplace transform of the output, and

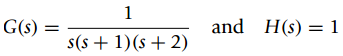
(a)?Find an expression for E(s) in terms of X(s), G(s), and H(s).

(b)?Let x(t) = u(t), and the Laplace transform of the corresponding error be E1(s). Use the final value property of the Laplace trans-form to obtain the steady-state error e1ss.

(c)?Let x(t) = tu(t), i.e., a ramp signal, and E₂(s) be the Laplace transform of the corresponding error signal. Use the final value property of the Laplace transform to obtain the steady-state error e_2ss. Is this error value larger than the one above? Which of the two inputs u(t) and r(t) is easier to follow?

(d)?Use MATLAB to find the partial fraction expansions of E₁(s) and E₂(s) and use them to find e₁(t) and e₂(t). Plot them.

Transcribed Image Text:

1 G(s) and H(s) = 1 s(s + 1)(s + 2)