In the following problems we use the inverse Laplace transform and the relation between input and output of LTI systems.

(a) The Laplace transform of the output of a system is

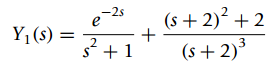
find y₁(t), assume it is causal.

(b) The Laplace transform of the output y₂(t)of a second-order system is

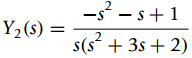
If the input of this system is x₂(t) = u(t), find the ordinary differential equation that represents the system and the corresponding initial conditions y₂(0) and dy₂(0)/dt.

(c) The Laplace transform of the output y(t)of a system is

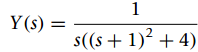
Assume y(t)to be causal. Find the steady-state response y_ss(t), and the transient y_t(t).

-2s (s + 2) + 2 (s + 2)° Y1 (s) = s* +1 3 -s - s+1 Y2(s) = s(s + 3s + 2)