The bounded-input bounded-output stability assumes that the input is always bounded, limited in amplitude. If that is not the case, even a stable system would provide an unbounded output. Consider the analog averager, with an input-output relationship

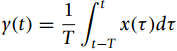
(a) Suppose that the input to the averager is a bounded signal x(t), i.e., there is a finite value M such that ˆ£x(t)ˆ£ < M. Find the value for the bound of the output y(t) and determine whether the averager is BIBO stable or not.

(b) Let the input to the averager be x(t) = t u(t), i.e., a ramp signal, compute the output y(t) and determine if it is bounded or not. If y(t) is not bounded, does that mean that the averager is an unstable system? Explain.

Н. x(т)dt У(0) : t-T