(a) Determine the compliance tensor S in terms of the elements of the cubic, or isotropic, elastic constant matrix C given in Table 3.1.

(b) If a uniaxial stress is applied along the [110] axis, what strain is created?

(c) Show that for an isotropic medium, if the direction of a uniaxial stress is originally along the x-axis, creating a strain, and then the direction of the stress is rotated about the y-axis by any angle θ, the strain created, relative to the new uniaxial stress axis, is still the same.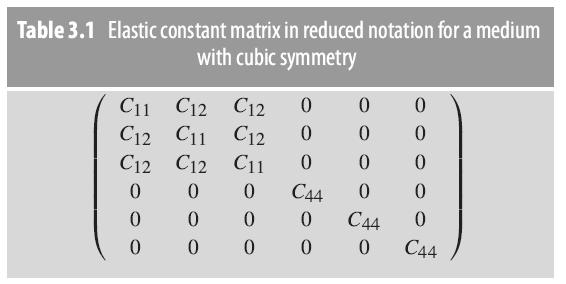

Table 3.1 Elastic constant matrix in reduced notation for a medium with cubic symmetry C11 C12 C12 C12 C11 C12 C12 C12 C11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 C44 0 0 0 0 0 C44 0 0 0 0 0 C44