(a) The GinzburgLandau equation can be written as where n 0 is the condensate density when ...
Question:
(a) The Ginzburg–Landau equation can be written as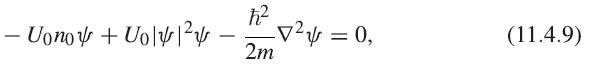
where n0 is the condensate density when ∇ψ = 0. Show that in the case of a straightline vortex with cylindrical symmetry, this can be written in unitless form as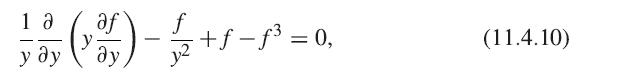
where y = r/r0, with r0 = h̄/√2mU0n0, and ψ = √n0eiθ f (r/r0). To do this, you should assume that the condensate phase θ is equal to the azimuthal angle ϕ everywhere.
(b) Use a program like Mathematica to solve this differential equation numerically for y from 0 to 5, with the boundary conditions f (0) = 0 and f (∞) = 1. The easiest way to do this is to use a “target shoot” method in which you solve the initial-value problem y(0) = 0, y′(0) = a, and pick values of the slope a until you hit the “target” of y(5) ≈ 1. Because of the singularity in the equation at y = 0, the numerical solution will be better behaved if you pick in initial value of y close to, but not exactly equal to 0, for example y = 0.01. In Mathematica, to generate the solution of the second-order differential equation you can use the NDSolve function, and then use the Table function to generate values of f (y) for specific y choices. You should be able to generate a plot like that shown in Figure 11.5.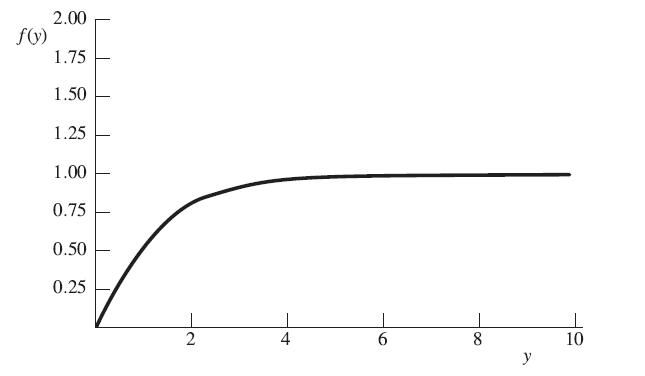
Step by Step Answer:






