Show that in the case when U(x) = 0 and u k = 1, that is, the
Question:
Show that in the case when U(x) = 0 and uk = 1, that is, the states are plane waves ψ = ei(kx−ωt) in a vacuum, and both k and ω are time-dependent, the solution of (2.8.14) for k = 0 at t = 0 implies k = qEt/h̄ and ω = (qEt)2/6h̄m.
Show that this implies that the average value of the energy, defined by
is equal to h̄2k2/2m. In other words, the kinetic energy grows in time in this case, and there is no Bragg reflection.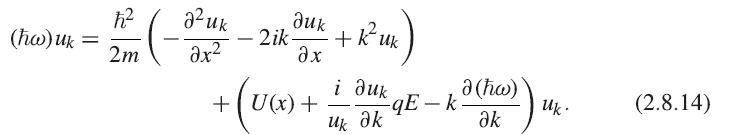
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





