Surprisingly, near a resonance, not only the phase velocity, but also the group velocitycan exceed the speed of light. This still does not violate the theory of relativity, because in the region near the resonance, the signal is strongly absorbed, so all that really happens is that a wave pulse is selectively absorbed on its trailing edge, which makes the leading edge appear to move faster than the speed of light.

To see this effect, use (7.1.20) to obtain a relation for k_R as a function of ω. Then take the derivative of this function with respect to ω. The inverse of this derivative, dω/dk, is the group velocity. Plot the group velocity vs ω for c = 1, ω₀ = 10, Γ = 1, and q²N/ϵ₀mV = 1. You should see that away from the resonance on either side, the group velocity is less than 1, but very near the resonance, in the region of strong absorption, the group velocity becomes larger than c (= 1). This is easily done using a program like Mathematica. This effect has been seen in atomic systems with a sharp, strong resonance.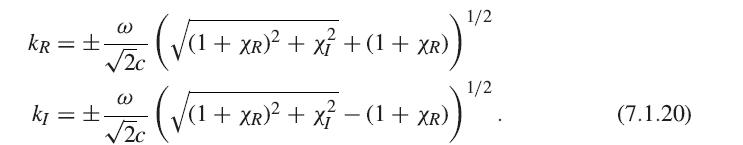

kR = k = @ 2c @ 2c ( (1 + XR) + x + (1 + XR) 1/2 (a 2 + XR))" (1 + XR) + x - (1 + XR) 1/2 (7.1.20)