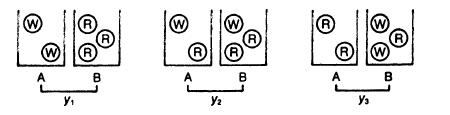
EXERCISE 5.1. Consider two pots, A and B, with three red balls and two white balls distributed between them so that A always has two balls and B always has three balls. There are three different configurations for the pots, as shown in the figure below. We obtain transitions between these three configurations by picking a ball out of A at random and one out of B at random and interchanging them.

(a) Compute the transition matrix Q and the conditional probability P|1(m, so|n, s).

(b) If initially Pi(1, 0) = 1, P(2, 0) = 0, and P (3, 0) = 0, compute the probability P(n, s) (n = 1, 2, and 3) at time s.

(c) Assume that the realization, y(n) = =n. Compute the first moment, (y(s)), and the autocorrelation function, (y(0)y(s)), for the same initial conditions as in part (b).

(W) A (R) (W) (W (R) (W) R R B A B A R (W) B Y2