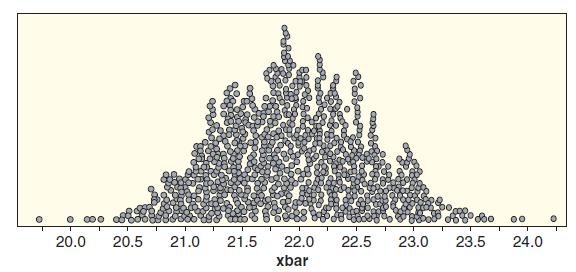
A distribution of bootstrap means for commuting times in St. Louis is given in Figure 5.13. As in Exercise 5.36, we use a N(21.97, 0.65) distribution as a reasonable model for these bootstrap means. Find the first and third quartiles of this normal distribution. That is, find a time (Q₁) where about 25% of the bootstrap means are below it and a time (Q₃) that is larger than about 75% of the bootstrap means.

Figure 5.13

Exercise 5.36

A bootstrap distribution of mean commute times (in minutes) based on a sample of 500 St. Louis workers stored in CommuteStLouis is shown in Figure 5.13. The pattern in this dotplot is reasonably bell-shaped so we use a normal curve to model this distribution of bootstrap means. The mean for this distribution is 21.97 minutes and the standard deviation is 0.65 minutes. Based on this normal distribution, what proportion of bootstrap means should be in each of the following regions?

Transcribed Image Text:

20.0 22.0 20.5 21.0 21.5 22.5 23.0 23.5 24.0 xbar ఆక