The variance of a probability distribution of a random variable is a weighted average of its squared distances from the mean m. For discrete random variables, it equals σ²= Σ(x - μ)²P(x). Multiply each possible squared deviation (x - μ)²by its probability P(x) and then add. The standard deviation σ is the positive square root of the variance. The table below shows the probability distribution for the number of games played in a best of seven series when each team has a 50% (taken from Example 2) or 99% chance of winning a game.

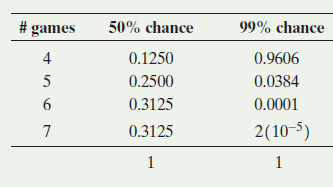
a. Find the standard deviation of X = number of games played to determine a winner when each team has a 50% chance of winning a game. (In Example 3, the mean was found to be equal to 5.8125.)
b. The table also shows the probability distribution when one team has a 99% chance of winning each game. Would you expect the standard deviation for this distribution to be smaller or larger than the one in part a? 

Transcribed Image Text:

# games 50% chance 99% chance 4 0.1250 0.9606 0.2500 0.0384 6. 0.3125 0.0001 2(10-5) 0.3125