Thirty students are asked to choose a random number between 0 and 9, inclusive, to create a dataset of n = 30 digits. If the numbers are truly random, we would expect about three 0€™s, three 1€™s, three 2€™s, and so on. If the dataset includes eight 7€™s, how unusual is that? If we look exclusively at the number of 7€™s, we expect the proportion of 7€™s to be 0.1 (since there are 10 possible numbers) and the number of 7€™s to be 3 in a sample of size 30. We are testing H₀: p = 0.1 vs H_a: p ‰  0.1, where p is the proportion of 7€™s. We can generate the randomization distribution by generating 1000 sets of 30 random digits and recording X = the number of 7€™s in each simulated sample.
SeeFigure 4.21.

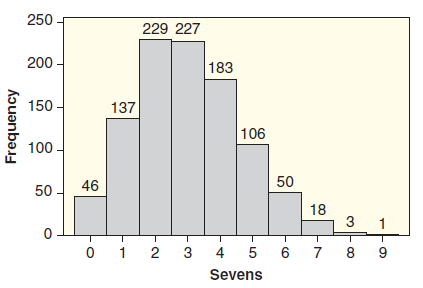
(a) Notice that this randomization distribution is not symmetric. This is a two-tailed test, so we need to consider both €˜€˜tails.€ How far is X = 8 from the expected value of 3? What number would be equally far out on the other side? Explain why it is better in this situation to double the observed one-tailed p-value rather than to add the exact values on both sides.

(b) What is the p-value for the observed statistic of X = 8 sevens when doing the two-tailed test?

(c) The randomization distribution in Figure 4.21 would apply to any digit (not just 7€™s) if the null hypothesis is H₀: p = 0.1. Suppose we want to test if students tend to avoid choosing zero when picking a random digit. If we now let p be the proportion of 0€™s all students choose, the alternative would be H_a: p < 0.1. What is the smallest p-value we could get using the randomization distribution in Figure 4.21? What would have to happen in the sample of digits from 30 students for this p-value to occur?

Transcribed Image Text:

250 - 229 227 200 - 183 150 - 137 106 100 - 50 46 50 18 3 1 2 3 Sevens Frequency