Question: Two 2 x 2 matrices, A and B, whose product is the multiplicative identity matrix are said to be multiplicative inverses. That is, if A

Two 2 x 2 matrices, A and B, whose product is the multiplicative identity matrix are said to be multiplicative inverses. That is, if A x B = B x A = I, then A and B are multiplicative inverses. In parts (a) and (b) below, show that matrices A and B are multiplicative inverses.

(a)

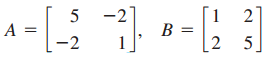
1 27 5 -2 A = -2 B = 2 5

(b)

3 [7 A = 1 -3 B = -2 7.

1 27 5 -2 A = -2 B = 2 5 3 [7 A = 1 -3 B = -2 7.

Step by Step Solution

★★★★★

3.40 Rating (172 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Thus A and B are multiplicative in... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Survey of Mathematics Questions!

The Process The production process: Homework - continued 1. Extrudes the polypropylene liner, cools and coils it. 2. Uncoils the liner, braids wire around it and recoils it. 3. Uncoils the wire...

Find two numbers whose sum is 32 and whose product is the maximum possible value.

Find two numbers whose sum is 20 and whose product is the maximum possible value.

(a) Show that, if A and B are commuting square matrices, then (A + B)2 = A2 + 2AB + B2. (b) Find a pair of 2 2 matrices A and B such that (A + B)2 + A2 + 2AB + B2.

4. Consider the system of linear equations below. 1 + 212 - 13 = 2 2x1 + 12 - 13 = 2 4x1 + 212 - 213 = 4 Create the augmented matrix [A b]. Row reduce the augmented matrix to row reduced Ech- elon...

Some help on these questions... much appreciated! Give two distinct 2 x 2 matrices, A and B, whose product is the zero matrix. That is, AB =0 and neither A nor B is the zero matrix.Prove that for any...

(b) Prove that for any two distinct invertible 2 x 2 matrices, A and B, their product cannot be the zero matrix. [2 marks] (c) Below are three invertible matrices P, Q and R. 3 O 2 3 P = Q = 2 5 R =...

1. Find the equation of the fourth order polynomial y(o:) = (13:4 -l- bass + 03:2 + do: + e that passes through the ve data points (1,1), (1, 9), (0,6), (2, 28) and (2, 0). (a) Derive the system of...

Let A, B be two 2 x 2 matrices. Which one of the following is true. (a) If A? = 0, then A = 0, where 0 is the 2 x 2 zero matrix. (b) If A? = A, then A = 0 or A = I2, where I, is the 2 x 2 identity...

Safari File Edit View History Bookmarks Window Help O US Q 8 0 Thu Dec 14 3:01 AM mylab.pearson.com C G My Grade.. B https://le.. My Grade. B https://le.. Sign in to... P Assignme... P Quiz CH 4...

Branger Ltd. has the choice of issuing floating-rate debt at LIBOR + 1% or fixed-rate debt at Swaps 6%. Likewise, Creeson Plastics can issue floating-rate debt at LIBOR + 2.5% or fixed-rate debt at...

An incandescent light bulb is the most common source of light produced by electrical energy. A current is made to flow through a wire, called a filament. Since this wire has resistance, the wire...

According to the article, what was the following day's effect of the earnings report on Apple's stock price? It had no significant impact on Apple's stock price. O It caused Apple's stock price to...

1. What types of mobile marketing tools/contents have you experienced in the meeting and event industry?

At a large university, the probability that a student takes calculus and is on the deans list is 0.042. The probability that a student is on the deans list is 0.21. Find the probability that the...

Below is given the summary from the 112th Congress of Senators whose terms end in 2013, 2015, or 2017. Choose one of these Senators at random and find a. P(Democrat and term expires in 2015) b....

In a pizza restaurant, 95% of the customers order pizza. If 65% of the customers order pizza and a salad, find the probability that a customer who orders pizza will also order a salad.

I want to know how is g= 0.085 Please explain me Value line shows that Honda Motor pays a dividend of 0.90 I in 2009 and they increase to 1.15 in expected 2011 - 2013. Then we can interpolate the...

Need Help Please Belief in Haunted Places A random sample of 285 college students were asked if they believed that places could be haunted, and 112 responded yes. Estimate the true proportion of...

A project your firm is considering requires an investment today of $ 5 8 , 0 0 0 and is forecasted to generate a cash flows starting one year from today of $ 5 9 6 2 per year forever. If the...