Show that having the exact value for the estimated sensor bandwidth is not required for the experimental process to find KEst discussed in Section 10. 4.3.4. In Experiment 10E, corrupt the value of the sensor bandwidth by changing it from 20 to 30 Hz (top node of GSEst block); be careful to restore the value to 20 before saving the file, because changing the value of a node permanently modifies the mud file.

a. Adjust KEst to minimize error signal, EO.

b. What conclusion can you draw?

Transcribed Image Text:

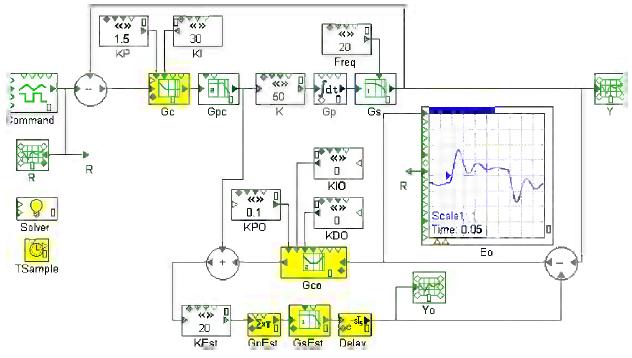
10.4.3.4 Experiment 10E: Determining the Gain Experimentally As discussed in Section 10.4.3.1, the plant scaling gain can be determined experimentally. The process to do this is simple and can be executed with an ordinary Luenberger observer, assuming the observer error signal (the input to the observer compensator) is available and that there are no significant disturbances to the control loop during this process. The system should be configured as follows: 1. Configure the observer estimated sensor and plant. Use the best guess available for the estimated plant scaling gain. 2. Configure the system to close the control loop on the sensor feedback (not the observed feedback). 3. Set the observer gains to very low values. 4. Minimize disturbances or operate the product-process in regions where disturbances are not significant. (Disturbances reduce the accuracy of this procedure.) 5. Excite the system with fast-changing commands. 6. Monitor Eo(s), the observer error. 7. Adjust the estimated plant scaling gain until the observer error is minimized. Experiment 10E modifies the model of Experiment 10C for this procedure. The estimated sensor is accurate; the estimated plant less the scaling gain is also configured accurately. Only the scaling gain is in error (20 here, instead of 50). The observer error, Eo(s), has large excursions owing to the erroneous value of KEst. The result is shown in Figure 10.16. The effect of changing the estimated scaling gain is shown in Figure 10.17. If KEst is either too large (a) or too small (c), the error signal is larger. The center (b) shows KEst adjusted correctly (KEst = 50). Only when Kest is adjusted correctly is Eo minimized.