(a) Determine the coherence area for a mercury arc lamp at 6330 at a distance of...

(a) Determine the coherence area for a mercury arc lamp at 6330 Ȧ at a distance of \(1 \mathrm{~m}\) from the source. Assume that the output aperture is \(3 \mathrm{~mm}\) and that the beam is diffraction-limited.

(b) If a \(30 \mu \mathrm{m}\) pinhole is placed in front of the lamp, what is the effect on the results in part (a)?

(c) Calculate the coherence diameter for setups (a) and (b) compare them with the spot size of a diffraction-limited beam. The coherence diameter \(d_{\text {coh }}\) is defined as the observation point separation where \(\left|\gamma_{12}ight|=0.88\), which translated into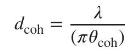

Transcribed Image Text:

dcoh ( con) coh.