Consider the following linear programming problem: where is randomly distributed with = 3 and 2 = 1. Give the chance constraint formulation

Consider the following linear programming problem:

where ξ is randomly distributed with μ = 3 and σ² = 1. Give the chance constraint formulation of the problem, and find the optimal solution.

Consider a reservoir that supplies water to a city. The monthly water demand of this complex is 20 million cubic meters. The total capacity of the reservoir is 40 million cubic meters. Let St (reservoir storage at the beginning of month t) take the discrete values 0, 10, 20, 30, and 40. The cost of operation (Loss) can be estimated as a function of the difference between release (Rt) and water demand as follows:

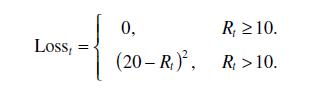
i. Formulate a forward-moving deterministic DP model for finding the optimal release in the next 3 months. ii. Formulate a backward-moving deterministic DP model for finding the optimal release in the next 3 months. iii. Solve the DP model developed in part (a), assuming that the inflows to the reservoir in the next 3 months (t = 1, 2, 3) are forecasted to be 10, 50, and 20, respectively. The reservoir storage in the current month is 20 million cubic meters.

Maximize Subject to x1 + x2, 2x + x x x+23,