Refer to the introduction to Problem 2.8 and the figure in Problem 2.9. Using the small angle approximation, develop an expression for wavelength used in this experiment. A pair of screens are placed \(13.7 \mathrm{~m}\) apart. A third order fringe is seen on the screen \(2.50 \mathrm{~cm}\) from the central fringe. Does the scatter angle a value consistent with the small angle approximation? If the slits were cut \(0.0960 \mathrm{~cm}\) apart, determine the wavelength of this light.

Problem 2.8

In Young's double-slit experiment, light intensity is a maximum when the two waves interfere constructively. This occurs when

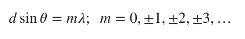
where \(d\) is the separations of the slits, \(\lambda\) the wavelength of light, \(m\) the order of the maximum, and \(\theta\) the scatter angle that the maxima occurs. Assume \(d=0.320 \mathrm{~mm}\). If a beam of \(\lambda=500 \mathrm{~nm}\) light strikes the two slits, how many maxima will there be in the angular range \(45^{\circ} \leq \theta \leq 45^{\circ}\) ?

Figure in Problem 2.9

Transcribed Image Text:

d sin 0 m; m = 0, +1, +2, +3,...