Analog signals abound, but in todays technological world, analog signals must be transformed into digital formats to

Question:

Analog signals abound, but in today’s technological world, analog signals must be transformed into digital formats to ease electronic transmission and processing. At the end, these digital signals are often restored to analog form. The first step in the conversion process uses a sample-and-hold circuit. This circuit is usually found at the input to an analog-to-digital converter (ADC). The purpose of the circuit is to sample an analog time-varying input waveform at a specified instant and then hold that value constant until conversion to digital form is complete. This example discusses the role of a capacitor in such a circuit.

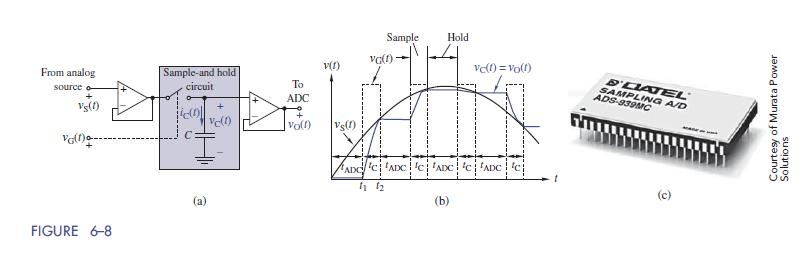
The basic sample-and-hold circuit in Figure 6–8

(a) includes an input buffer, a digitally controlled electronic switch (usually driven by a digital clock υGðtÞ), a holding capacitor C, and an output buffer. The input buffer is a voltage follower whose output replicates the analog input signal υSðtÞ and prevents the sample-and-hold circuit from loading the input. Importantly, the input buffer supplies a charging current iCðtÞ to the capacitor. The output buffer is also a voltage follower whose output replicates the capacitor voltage and prevents the ADC circuit from loading the sample-andhold circuit To see how the circuit operates, we describe one cycle of the sample-and-hold process. At time t1 shown in Figure 6–8(b), the digital control υGðtÞ goes high, which causes the switch to close. This act allows the input buffer to supply a charging current iCðtÞ to drive the capacitor voltage to the level of the analog input. At time t2 also shown in Figure 6–8(b), the digital control goes low, the switch opens, and thereafter the capacitor current iCðtÞ = 0. Zero current means that capacitor voltage is constant since dvCðtÞ=dt is zero. In sum, closing the switch causes the capacitor voltage to track the input (once the capacitor reaches that value), and opening the switch causes the capacitor voltage to hold a sample of the input until the process repeats.

Figure 6–8

(b) shows several more cycles of the sample-and-hold process. Samples of the input waveform are acquired during the time intervals labeled tC. During these intervals the control signal is high, the switch is closed, and the capacitor charges or discharges in order to track the analog input voltage. Analog-to-digital conversion of the circuit output voltage takes place during the time intervals tADC. During these intervals the control signal is low, the switch is open, and the capacitor holds the output voltage constant.

Sample-and-hold circuits are available as monolithic integrated circuits (see Figure 6–8(c)) that include the two buffers, the electronic switch, but usually not the holding capacitor. The capacitor is supplied externally, and its selection involves a trade-off. In an ideal sample-and-hold circuit, the capacitor voltage tracks the input when the switch is closed (sample mode) and holds the value indefinitely when the switch is open (hold mode). In real circuits the input buffer has a maximum output current, which means that some time is needed to charge the capacitor in the sample mode. Minimizing this sample acquisition time argues for a small capacitor. On the other hand, in the hold mode, the output buffer draws a small current that gradually discharges the capacitor, causing the output voltage to slowly decrease. Minimizing this output drop calls for a large capacitor. Thus, selecting the capacitance of the holding capacitor involves a compromise between the sample acquisition time and the output voltage drop in the hold mode. A few other issues might be obvious. The capacitor must have sufficient time to charge up to the value of the signal, hence the clock signal must be sufficiently long to permit this to happen. Similarly, the time allowed for the conversion to occur must also be sufficient. Note also that the analog signal shown is changing slowly. Clearly if the analog signal was changing more rapidly, then the sampling and conversion must be done faster. Currently these concerns are beyond the scope of this text, but for those interested, investigate Nyquist and Sampling Theory or see Example 13–12 in this text.

image text in transcribed